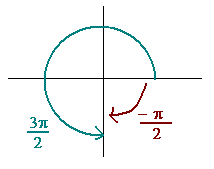You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
restrictions
- Thread starter mathfun
- Start date
mathfun said:Determine the restrictons:
cotx/(1+sinx)
I understand the restrictons: sinx cannot=o, -1
but in the answers, it also has.. "for o<_x < 2pi, x cannot= o, pi, (3pi)/2.
how do u get those values?
You are correct. Now solve for x.
In the domain 0 to 2pi:
sin(x) = 0 --> x = 0, pi
sin(x) = -1 --> x = 3pi/2
stapel said:Why can the sine not be zero? Or did you mean that x can't be zero? If so, then why can't x be -1?
sinx cannot be zero because
cotx
--------
1+sinx
= (cosx/sinx)/(1+sinx)
=1/(sinx)(1-sinx)
Unco said:mathfun said:Determine the restrictons:
cotx/(1+sinx)
I understand the restrictons: sinx cannot=o, -1
but in the answers, it also has.. "for o<_x < 2pi, x cannot= o, pi, (3pi)/2.
how do u get those values?
You are correct. Now solve for x.
In the domain 0 to 2pi:
sin(x) = 0 --> x = 0, pi
sin(x) = -1 --> x = 3pi/2
if i'm looking for restrictons of sinx i have to solve for x, which wuld be the restrictions as well?
The question didn't ask for the restrictions of sin(x), as such; "determine the restrictions" is probably best read "Determine which values of x result in the expression being undefined".
Think of the annoying examiner who has to act like he or she doesn't know anything except what's written in the answer schedule: the examiner doesn't know what \(\displaystyle \sin{x} \, \neq \, 0, \, - 1\) means because the answers are in terms of x, so your best bet is to take it all the way and say \(\displaystyle x \, \neq \, 0, \, \pi, \, \frac{3\pi}{2}\) (for \(\displaystyle 0 \, \leq \, x \, \leq \2\pi\)) and get your deserved marks.
Think of the annoying examiner who has to act like he or she doesn't know anything except what's written in the answer schedule: the examiner doesn't know what \(\displaystyle \sin{x} \, \neq \, 0, \, - 1\) means because the answers are in terms of x, so your best bet is to take it all the way and say \(\displaystyle x \, \neq \, 0, \, \pi, \, \frac{3\pi}{2}\) (for \(\displaystyle 0 \, \leq \, x \, \leq \2\pi\)) and get your deserved marks.
Hello, mathfun!
It's simpler than you think . . .
\(\displaystyle \;\;\cot x\) is undefined for \(\displaystyle x\,=\,0,\,\pi.\;\;\)Hence: \(\displaystyle \,x\,\neq\,0,\,\pi\)
\(\displaystyle \;\;\)Since the denominator cannot be zero: \(\displaystyle \,\sin x\,\neq\,-1\;\;\Rightarrow\;\;x\,\neq\,\frac{3\pi}{2}\)
It's simpler than you think . . .
Restricting the domain to: \(\displaystyle 0\,\leq\,x\,<\,2\pi\) . . .Determine the restrictons: \(\displaystyle \L\,\frac{\cot x}{1\,+\,\sin x}\)
\(\displaystyle \;\;\cot x\) is undefined for \(\displaystyle x\,=\,0,\,\pi.\;\;\)Hence: \(\displaystyle \,x\,\neq\,0,\,\pi\)
\(\displaystyle \;\;\)Since the denominator cannot be zero: \(\displaystyle \,\sin x\,\neq\,-1\;\;\Rightarrow\;\;x\,\neq\,\frac{3\pi}{2}\)
- Joined
- Feb 4, 2004
- Messages
- 16,582
Thanks. I'd misread the numerator as being a cosine, not a cotangent.mathfun said:sinx cannot be zero because...
Eliz.
soroban said:Hello, mathfun!
It's simpler than you think . . .
Restricting the domain to: \(\displaystyle 0\,\leq\,x\,<\,2\pi\) . . .Determine the restrictons: \(\displaystyle \L\,\frac{\cot x}{1\,+\,\sin x}\)
\(\displaystyle \;\;\cot x\) is undefined for \(\displaystyle x\,=\,0,\,\pi.\;\;\)Hence: \(\displaystyle \,x\,\neq\,0,\,\pi\)
\(\displaystyle \;\;\)Since the denominator cannot be zero: \(\displaystyle \,\sin x\,\neq\,-1\;\;\Rightarrow\;\;x\,\neq\,\frac{3\pi}{2}\)
how would i find out that cotx is undefined for x = pi
sinx /= -1...how does that get x /= 3pi/2?
because sinx /=-1 ..should make sinx/= - pi=2....
You've demonstrated that you know cot(x) = cos(x)/sin(x), so is undefined when sin(x) = 0. And sin(x) = 0 when x=0, pi, in the domain 0<x<2pi. This has been covered.mathfun said:how would i find out that cotx is undefined for x = pi
A thread or two ago you appeared to demonstrate you know that sin(x) = -1 when x=3pi/2 in the domain 0<x<2pi.mathfun said:sinx /= -1...how does that get x /= 3pi/2?
because sinx /=-1 ..should make sinx/= - pi=2
-pi/2 and 3pi/2 are 2pi apart so are equivalent.
...0 being a restriction..what does that have anything to do with pi?Unco said:You've demonstrated that you know cot(x) = cos(x)/sin(x), so is undefined when sin(x) = 0. And sin(x) = 0 when x=0, pi, in the domain 0<x<2pi. This has been covered.mathfun said:how would i find out that cotx is undefined for x = pi
A thread or two ago you appeared to demonstrate you know that sin(x) = -1 when x=3pi/2 in the domain 0<x<2pi.mathfun said:sinx /= -1...how does that get x /= 3pi/2?
because sinx /=-1 ..should make sinx/= - pi=2
-pi/2 and 3pi/2 are 2pi apart so are equivalent.[/quote]
then how come -pi/2 is not part of the restrictions?
mathfun said:...0 being a restriction..what does that have anything to do with pi?Unco said:You've demonstrated that you know cot(x) = cos(x)/sin(x), so is undefined when sin(x) = 0. And sin(x) = 0 when x=0, pi, in the domain 0<x<2pi. This has been covered.mathfun said:how would i find out that cotx is undefined for x = pi
sin(pi) = 0
A thread or two ago you appeared to demonstrate you know that sin(x) = -1 when x=3pi/2 in the domain 0<x<2pi.mathfun said:sinx /= -1...how does that get x /= 3pi/2?
because sinx /=-1 ..should make sinx/= - pi=2
-pi/2 and 3pi/2 are 2pi apart so are equivalent.
then how come -pi/2 is not part of the restrictions?
0 < x < 2pi was arbitrariliy chosen to be the domain. -pi/2 is outside this domain.
[/quote]Unco said:A thread or two ago you appeared to demonstrate you know that sin(x) = -1 when x=3pi/2 in the domain 0<x<2pi.mathfun said:sinx /= -1...how does that get x /= 3pi/2?
because sinx /=-1 ..should make sinx/= - pi=2
-pi/2 and 3pi/2 are 2pi apart so are equivalent.
then how come -pi/2 is not part of the restrictions?
0 < x < 2pi was arbitrariliy chosen to be the domain. -pi/2 is outside this domain.
since sinx=-1 and x will equal -pi/2....what will i have to do to -pi/2 to get 3pi/2?
also..what about pi/2...isn't it a restriction as well?