StarlitxSunshine
New member
- Joined
- Nov 15, 2009
- Messages
- 2
Here is the question & below are my steps. I have the answer, but I cannot seem to get to it.
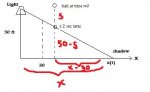
A light shines from the top of a pole 50 ft high. A Ball is dropped from the same height from a paoint 30 ft away from teh light as shown below. How fast is the ball's shadow moving along the ground 1/2 sec later?
(Assume the ball falls a distance s=16t^2 in t sec)
dx/dt = ?
s= 16^2
t= 1/2
I set up a proportion as the equation:
50/50-s = x/x-30
50x-1500 = 50x -sx
Then differentiated to find related rates:
50dx/dt = 50 dx/dt - sdx/dt
But here, even with simplication, I end up with:
sdxt/dt = 0
-16(1/2)^2 * dx/dt = 0
dx/dt will equal zero. When the answer is supposed to be -150 m/s
What am I doing wrong, please ?
A light shines from the top of a pole 50 ft high. A Ball is dropped from the same height from a paoint 30 ft away from teh light as shown below. How fast is the ball's shadow moving along the ground 1/2 sec later?
(Assume the ball falls a distance s=16t^2 in t sec)
dx/dt = ?
s= 16^2
t= 1/2
I set up a proportion as the equation:
50/50-s = x/x-30
50x-1500 = 50x -sx
Then differentiated to find related rates:
50dx/dt = 50 dx/dt - sdx/dt
But here, even with simplication, I end up with:
sdxt/dt = 0
-16(1/2)^2 * dx/dt = 0
dx/dt will equal zero. When the answer is supposed to be -150 m/s
What am I doing wrong, please ?