Jakotheshadows
New member
- Joined
- Jun 29, 2008
- Messages
- 47
"Two carts, A and B, are connected by a rope 39 feet long that passes over a pulley P (I will do my best to provide the figure given in the text). The point Q is on the floor 12 feet directly beneath P and between the carts. Cart A is being pulled away from Q at a speed of 2 ft/s. How fast is cart B moving toward Q at the instant when cart A is 5 ft from Q?"
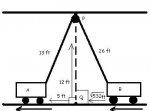
[attachment=0:jk40p3c4]Related Rates.JPG[/attachment:jk40p3c4]
This is my depiction of the figure given with the problem with the addition of some of my work included.
The rope lengths from carts A and B to pulley P, and the distance from cart B to point Q when cart A is 5 ft from Q are additions I have made to the depiction of the textbook figure from my own work.
I let A = the distance from cart A to Q
I let B = the distance from cart B to Q
I let H = the height of the triangle formed by the rope and the distance (which is equal to A+B) between the two carts.
I used the Pythagorean theorem to solve for the rope lengths on each side of the pulley when cart A is 5 ft from Q.
12^2 + 5 ^2 = 169 --> (169)^.5 = 13.
The rope is 39 ft long, so the rope segment connecting the pulley P to cart B must be 39 - 13 = 26 ft.
I used the Pythagorean theorem again to solve for the distance between point Q and cart B.
12^2 + B^2 = 26^2 --> B^2 = 532 --> B = (532)^.5
I let dA/dt be the change in A with respect to t (time) which is given as 2 ft/s in the text.
I let dB/dt be the change in B with respect to t which is the unknown.
I can't seem to think of an equation to relate these two rates. There is some geometry here that eludes me. Can anyone help fill in the next step which is blank in my mind at the moment?
[attachment=0:jk40p3c4]Related Rates.JPG[/attachment:jk40p3c4]
This is my depiction of the figure given with the problem with the addition of some of my work included.
The rope lengths from carts A and B to pulley P, and the distance from cart B to point Q when cart A is 5 ft from Q are additions I have made to the depiction of the textbook figure from my own work.
I let A = the distance from cart A to Q
I let B = the distance from cart B to Q
I let H = the height of the triangle formed by the rope and the distance (which is equal to A+B) between the two carts.
I used the Pythagorean theorem to solve for the rope lengths on each side of the pulley when cart A is 5 ft from Q.
12^2 + 5 ^2 = 169 --> (169)^.5 = 13.
The rope is 39 ft long, so the rope segment connecting the pulley P to cart B must be 39 - 13 = 26 ft.
I used the Pythagorean theorem again to solve for the distance between point Q and cart B.
12^2 + B^2 = 26^2 --> B^2 = 532 --> B = (532)^.5
I let dA/dt be the change in A with respect to t (time) which is given as 2 ft/s in the text.
I let dB/dt be the change in B with respect to t which is the unknown.
I can't seem to think of an equation to relate these two rates. There is some geometry here that eludes me. Can anyone help fill in the next step which is blank in my mind at the moment?