Reimann Sum

[CatchThis2]

F(x)=-x^2/6 + 2x on the interval 3,7

The value of the left endpoint of the reimann sum is?

I am not sure if this has to be integrated or if I just plug values in from 3 to 6.5.

 

[galactus]

Are you being asked to use the left endpoint method and the Riemann sum to find the area under the curve as if you

integrated the easy way?. It would also appear they just want you to identify the left endpoint. A Riemann sum is how

integration works. You add up the area of the infinite number of

rectangles under the curve. This is rather tedious because of the algebra. You also need to know the summation

identities. f(x) is the height of the rectangle and dx is the width. Add up all their areas and you get the area under the

curve. That is why we add all them up and take the limit as the number of rectangles increases toward infinity.

See the idea?.

\(\displaystyle dx={\Delta}x=\frac{b-a}{n}=\frac{7-3}{n}=\frac{4}{n}\)

The left point method starts with \(\displaystyle x_{k}=a+(k-1){\Delta}x\Rightarrow 3+4(k-1)\cdot \frac{4}{n}=\frac{4k+3n-4}{n}\)

Plug this in for x as if you are setting up an integral f(x)dx.

\(\displaystyle f(x_{k}){\Delta}x=\left[\frac{-\left(\frac{4k+3n-4}{n}\right)^{2}}{6}+2\left(\frac{4k+3n-4}{n}\right)\right]\cdot\frac{4}{n}\)

Expand out using algebra, then sum:

\(\displaystyle \frac{-32}{n^{3}}\sum_{k=1}^{n}k^{2}+\frac{16}{n^{2}}\sum_{k=1}^{n}k+\frac{64}{n^{3}}\sum_{k=1}^{n}k+\frac{18}{n}\sum_{k=1}^{n}1-\frac{16}{n^{2}}\sum_{k=1}^{n}1-\frac{32}{3n^{3}}\sum_{k=1}^{n}1\)

Now, using the identities, \(\displaystyle \sum_{k=1}^{n}k^{2}=\frac{n(n+1)(2n+1)}{6}, \;\ \sum_{k=1}^{n}k=\frac{n(n+1)}{2}, \;\ \sum_{k=1}^{n}1=n\) sub them in and do the tedious algebra. It will be entirely in terms of n with no k's.

It should whittle down to something with n's in the denominator and a constant.

Thereby, taking the limit as \(\displaystyle n\to {\infty}\), the constant is all that remains and that is the area you need.

If done correctly, you should get 202/9

 

[mmm4444bot]

F(x)=-x^2/6 + 2x on the interval 3,7

The value of the left endpoint of the reimann sum is? A Riemann Sum does not have "endpoints" itself, but the intervals used to set-up a Riemann Sum each have endpoints.

I am not sure if this has to be integrated or if I just plug values in from 3 to 6.5. I'm not sure, either, because you did not provide the instructions that came with this exercise.

Also, where did 6.5 come from?

Did they ask you to estimate the area underneath the graph of F(x) from x = 3 to x = 7 by using eight rectangles with width 0.5 units?

If so, then you need to calculate the height of each of these rectangles.

Using the left endpoint of each interval, the heights of the eight rectangles are:

F(3)
F(3.5)
F(4)
F(4.5)
F(5)
F(5.5)
F(6)
F(6.5)

Multiplying each height by 0.5 gives the area of each rectangle.

Adding these eight areas yields a Reimann Sum, which is an estimate of the area underneath the curve of F(x) from x = 3 to x = 7.

But, like Galactus, I'm only guessing at what you've actually been asked to do.

[attachment=0:2p14nm05]RS.JPG[/attachment:2p14nm05]

 

[CatchThis2]

The rectangles in the graph below illustrate a left endpoint Riemann sum for fraction -x^2/6 + 2 x on the interval (3, 7)
The value of this left endpoint Riemann sum is______ , and this Riemann sum is an the area of the region enclosed by y = f(x), the x-axis, and the vertical lines x = 3 and x = 7.

 

[galactus]

Then they are asking for the area as I outlined above. Looks ominous, huh?. :wink:

Since they did not give the number of intervals, then we use n of them. As n gets larger and larger, the actual area under the curve is approached.

It's not, once you get the concept of an integral. Reimann sums help show what an integral does.

Google and you can find lots. Your calc text will also have it detailed. It should, anyway.

 

[CatchThis2]

They are asking for the area. Looking all over at internet tutorials and my notes but still no luck on solving.

 

[mmm4444bot]

The rectangles in the graph below illustrate a left-endpoint Riemann sum This statement implies that you have an illustration that goes with this exercise.

How many rectangles do you count, in that illustration?

The value of this left-endpoint Riemann sum is______ This makes more sense than what you originally posted. (Note that I hyphenated their compound adjective, for them.)

So, their pronoun "this" refers to the sum of rectangle areas in the illustration they referenced, yes?

and this Riemann sum is an the area of the region enclosed by y = f(x), the x-axis, and the vertical lines x = 3 and x = 7

Come on! (heh, heh) You may not use both an indefinite and a definite article simultaneously. Either they are telling you that it's the exact area or they are telling you that it's one of many estimated areas.

"an area" means one of many estimates.

"the area" means the exact area.

Which is it?

My best guess is the same, that the number of rectangles is not becoming infinite, in your exercise. (How would they draw that?)

If they gave you a fixed number of rectangles to work with, the left-endpoint Riemann Sum is an estimate of the area underneath the curve of the function F(x).

The more rectangles you construct, between x = 3 and x = 7, the more precise the estimated area becomes, using Riemann Sums.

If you want the exact area, then you let the number of rectangles become infinite. As Galactus showed, it's awkward to work with infinite rectangles, using a Riemann Sum with infinite terms.

Please tell us what the illustration looks like. Is it similar to the illustration that I posted for you earlier?

How many rectangles do you see, in your illustration, under the curve of F(x)?

Where did the number 6.5 come from, in your first post?

If you would like more help from me, then you need to answer these three questions.

 

[mmm4444bot]

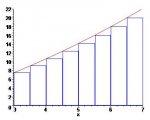
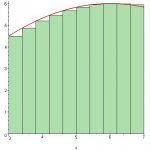
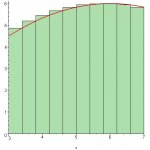
They are asking for the area. If it's true that they want "the" area, then Galactus set it up nicely, for you.

If they've actually given you a fixed number of rectangles to work with, then you are looking for "an" area, and it will be an estimate of the area underneath F(x), from x = 3 to x = 7.

Start by finding the height of each rectangle (i.e., the value of F(x), where x is located at the lower-left corner of each rectangle).

Looking all over at internet tutorials and my notes but still no luck on solving.

Try searching on keywords lesson left-endpoint riemann sum at Google. They have about 1,740 references.

More importantly, study what you see (in your notes and "all over" the Internet). I can't believe that you don't have any specific questions, for us. Yet, you've asked zero questions about your notes or lessons.

 

[CatchThis2]

I got the area to be 86.5 but for some reason that answer is incorrect and I plugged all the values into the equation from 3-6.5.

 

[galactus]

Again, where is this 6.5 coming from when the limits are 3 to 7?.

I think you better go see your instructor because from this one and your previous posts you seem to be missing basic concepts.

 

[CatchThis2]

I am using 6.5 because since it says left endpoint you should use 6.5 instead of 7. 7 would be a right hand endpoint.

 

[galactus]

Are they stating to break it up into a certain number of intervals?. I used infinite intervals using the left endpoint method. Which, as you can see, seems a little more complicated.

Besides, the midpoint method ues 1/2 taken from the lower limit.

 

[BigGlenntheHeavy]

\(\displaystyle f(x) \ = \ \int_{3}^{7}\bigg[-\frac{x^{2}}{6}+2x\bigg]dx \ = \ \frac{202}{9} \ = \ 22.\overline4\)

\(\displaystyle Here \ is \ the \ left \ endpoint \ when \ n \ = \ 10, \ ergo, \ g(x) \ = \ \frac{554}{25} \ = \ 22.16.\)

\(\displaystyle Note: \ As \ galactus \ pointed \ out, \ when \ n \ approaches \ infinity, \ f(x) \ approaches \ its \ true \ value.\)


[attachment=1:3schyjro]pqr.jpg[/attachment:3schyjro]

\(\displaystyle Below \ is \ the \ graph \ using \ the \ right \ endpoint \ when \ n \ = \ 10,\)

\(\displaystyle h(x) \ = \ \frac{1702}{75} \ = \ 22.69\overline3.\)

[attachment=0:3schyjro]stu.jpg[/attachment:3schyjro]

\(\displaystyle Note: \ g(x) \ < \ f(x) \ < \ h(x) \ when \ n \ = \ 10.\)

\(\displaystyle As \ n \ approaches \ infinity \ g(x) \ will \ = \ h(x), \ squeeze \ theorem \ anyone?\)

\(\displaystyle Another \ note: \ mmm4444bot \ graph \ is \ wrong \ as \ his \ equation \ is \ wrong.\)

 

[CatchThis2]

My question doesn't involve n=10 though. It only says find the sum for F(x)=-x^2/6+2x on the interval {3,7} which is the region enclosed by the vertical lines x=3 and x=7

 

[BigGlenntheHeavy]

Hey, pal, what is your problem? When n= 10, you get the above, when n approaches infinity, you get the true value. Need I be any more succinct? Do you suffer from some sort of mental impairment?


\(\displaystyle True \ Value: \ \int_{3}^{7}\bigg[-\frac{x^{2}}{6}+2x\bigg]dx \ = \ \frac{202}{9} \ = \ 22.\overline4.\)

 

[galactus]

It only says find the sum for F(x)=-x^2/6+2x on the interval {3,7} which is the region enclosed by the vertical lines x=3 and x=7

That is what I outlined in my first post. Did you read it?.

 

[mmm4444bot]

I'm not sure why the original poster will not answer questions about the illustration that goes with this exercise.

There is apparently some graph provided, on which a fixed number of rectangles has been drawn. The original poster refuses to tell us how many rectangles there are.

Why is it a secret? :?

 

[BigGlenntheHeavy]

mmm4444bot, I haven't the slightest idea where this guy is coming from, your guess is as good as mine.

 

[galactus]

No doubt. I think I am throwing in the towel.