This is from Kurzweil and Stellmacher, The Theory of Finite Groups, New York, 2004.
G is supposed to be finite and act transitively on \(\Omega\):
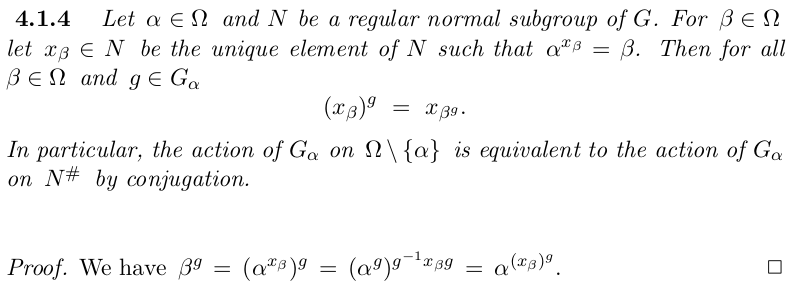
I don't understand the proof. From the equality I get \(\beta=\alpha^{{(x_{\beta})^g g^{-1}}}\). Unfortunately the exponent does not necessarily belong to N and so I can't use the uniqueness. Any suggestion?
G is supposed to be finite and act transitively on \(\Omega\):
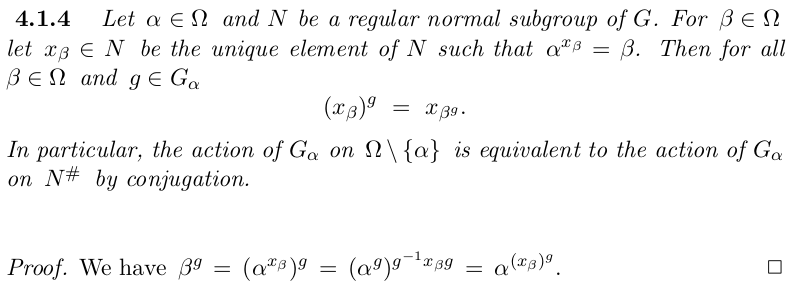
I don't understand the proof. From the equality I get \(\beta=\alpha^{{(x_{\beta})^g g^{-1}}}\). Unfortunately the exponent does not necessarily belong to N and so I can't use the uniqueness. Any suggestion?
