Hello,
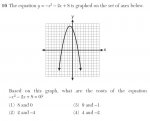
I have a question on an August 2009 regents question. It is asking me to find the root of an equation. I do not understand the question. The question also includes a graph which I am unable to upload on this post. The link for the website is http://nysedregents.org/IntegratedAlgebra/20090813examw.pdf. It is question number 16.
-Thank You
I have a question on an August 2009 regents question. It is asking me to find the root of an equation. I do not understand the question. The question also includes a graph which I am unable to upload on this post. The link for the website is http://nysedregents.org/IntegratedAlgebra/20090813examw.pdf. It is question number 16.
-Thank You