rectangle/ellipse maximum problem

[littlejodo]

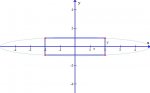
A rectangle with sides parallel to the coordinate axes is inscribed in the ellipse: 1x^2 +25y^2 = 25

Find the dimensions of the rectangle of greatest area:
x=
y=

The process I think I need to follow is to take the derivative of the equation (if this is really the equation I am supposed to use)
then solve for x
use values of x to find the maximum

But in this case we have x and y variables in play. Solving for y I got the following:
1x^2 +25y^2 = 25
x + 5y = 5 (square root all terms)
x - 5 = 5y
(x-5)/5 = y
but then when I take the derivative I just get :
1(5) - x-5(0) -- so that pretty much gives me the impression that I am on the wrong track.

If I take the implicit derivative:
1x^2 +25y^2 = 25
2x + 50y(dy/dx) = 0
2x = -50y(dy/dx)
2x/-50y = (dy/dx) -- but now I still have a y in the equation, which also makes me think I've done something wrong.

In the problem it states that the rectangle is "inscribed" in the ellipse, so maybe that means something that I don't understand.

Help????

 

[galactus]

I see your problem.

By now you should know that:

\(\displaystyle \sqrt{x^{2}+25y^{2}}\neq x+5y\)

It does not work that way.

Solving the ellipse equation for y, we get \(\displaystyle y=\pm\frac{\sqrt{25-x^{2}}}{5}\)

If we let the rectangle in the first quadrant have length x and height y, then the entire area is 4xy.

Do the subs, differentiate and solve for x. Then, you're on your way.

I just drew a rectangle in an ellipse to illustrate. It is not necessarily the correct dimensions.

The area of an ellipse can be gotten form the formula \(\displaystyle A_{e}={\pi}ab\). Where a is the length of the major axis and b the length of the minor axis.

In this case, a=5 and b=1. So, the area of the ellipse is \(\displaystyle {\pi}\cdot 5\cdot 1=5{\pi}\)

The ratio of the area of the largest rectangle inscribed and the area of the ellipse is \(\displaystyle \frac{2}{\pi}\)

See what you get and check against the ratio.

 

[littlejodo]

If we let the rectangle in the first quadrant have length x and height y, then the entire area is 4xy.

Do the subs, differentiate and solve for x. Then, you're on your way.

Forgive me, often times I'm very slow in understanding... If the area is 4xy, and y = +/- sqrt(25 - x^2) / 5 ... does that mean that the equation I am looking for is 4x(sqrt(25 - x^2) / 5 ) ?? I was thinking this might be the case since the entire area is 4xy.

If so, is this the "sub" I was supposed to do or am I missing something else?

I took this idea and then tried to differentiate:
4x(sqrt(25 - x^2) / 5 )
4(sqrt(25 - x^2) /5) + 4x ( 1/2(25 - x^2)^-1/2 (-2x)/[25] -- product, chain and quotient rule (I left off the terms made zero by the constant 5) except I wasn't sure about the "divided by bottom squared" when the bottom was a constant. I left that part in.

So in trying to combine stuff I came up with this:
4/5(sqrt(25-x^2) + 4x/25(-x(sqrt(25-x^2)
sqrt(25-x^2)[4/5 + 4x/25] -- factor out the sqrt(25-x^2)

SO then x = +/- 5

IF this is right, then when I put +/- 5 back into the derivative equation I end up with 0 both ways. This CAN'T be right. ugh. help? (again)?

 

[galactus]

Yes, that is the correct sub.

Area of rectangle: \(\displaystyle A=4x\left(\frac{\sqrt{25-x^{2}}}{5}\right)\)

Upon differentiating, we get \(\displaystyle \frac{dA}{dx}=\frac{100-8x^{2}}{5\sqrt{25-x^{2}}}\)

Set to 0 and solve for x. All we need is to set \(\displaystyle 100-8x^{2}=0\)

And find that \(\displaystyle x=\frac{5}{\sqrt{2}}\)

Sub this into the A equation to find the total area.

Now, you should be able to find the area.

 

[littlejodo]

Wow thank you!!

unfortunately, when I plug the value for x back into the area equation I get and answer that the online submission site says is wrong. this may never end

x = 5/sqrt2

I did the calculations on my calculator several times

4(5/sqrt2)((sqrt(25 - (5/sqrt2)^2)/5)) = 35.35533906

when I put it into a calculator on my computer for some reason I get the answer 10*sqrt(2) which is also wrong.

I get that it is the wrong answer. any ideas?

 

[galactus]

The total area is a nice integer. Did you use the area of an ellipse formula I mentioned to check.

You must have some arithmetic trouble.

\(\displaystyle 4(\frac{5}{\sqrt{2}})\frac{\sqrt{25-(\frac{5}{\sqrt{2}})^{2}}}{5}=\text{not what you got}\)

 

[littlejodo]

yes, when I put the formula directly into the submission box I got a 10.. which sounds great except it also fed back a "incorrect" message.

So I keep trying to make sure I'm not entering in the stuff wrong.

Is 10 what you came to as well??

 

[galactus]

Yes, that is what I got as well. Perhaps the rectangle is above the x-axis alone. I drew it above and below.

 

[xsoon2bprox]

I understand the whole problem except for one part. You said the area of the rectangle was A=4xy... were did the number 4 come from?

 

[skeeter]

I understand the whole problem except for one part. You said the area of the rectangle was A=4xy... were did the number 4 come from?

one rectangle with dimensions x by y in each quadrant ... 4 quadrants.

 

[xsoon2bprox]

so for the rectangle formed inside of an eclipse with a maximum area with the origin at (0,0) the area will be A=4xy for all rectangles?

 

[xsoon2bprox]

as in i would follow the same procedure for triangle with a maximum area in an eclipse y^2/144 + x^2/16 = 1

 

[skeeter]

so for the rectangle formed inside of an eclipse with a maximum area with the origin at (0,0) the area will be A=4xy for all rectangles?

yes

 

[dimleed]

Hi,

it is simpler to make the equation of the ellipse:

0.5 + 0.5 = 1 and calculate the numerators.

For sides a = 5 and b = 1, - or viceversa

0.5 * 25 = 12.5
0.5 * 1 = 0.5

take the square roots of these numbers as coordinates x and y so that

4xy is the area = 10