metastable
New member
- Joined
- Oct 18, 2020
- Messages
- 12
Hello,
I’ve been struggling to rearrange this formula which has to do with the geometry of a cycloid.
I want to rearrange this formula to solve for t but find it very difficult:
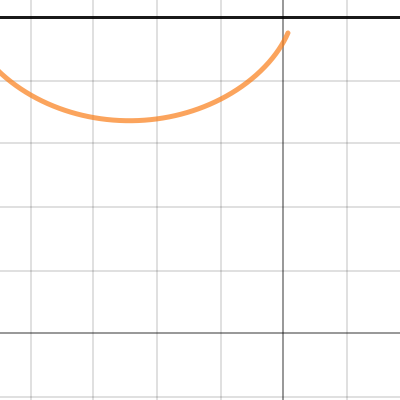
A=-(B/2(pi-t+sin(t)))(1-cos(t))
It has to do with the Brachistochrone problem of finding the ramp/path of quickest descent with no friction and only gravity, but with the added twist of having an initial velocity and the 2 points are horizontal to each other.
The way I’ve solved it so far is as follows:
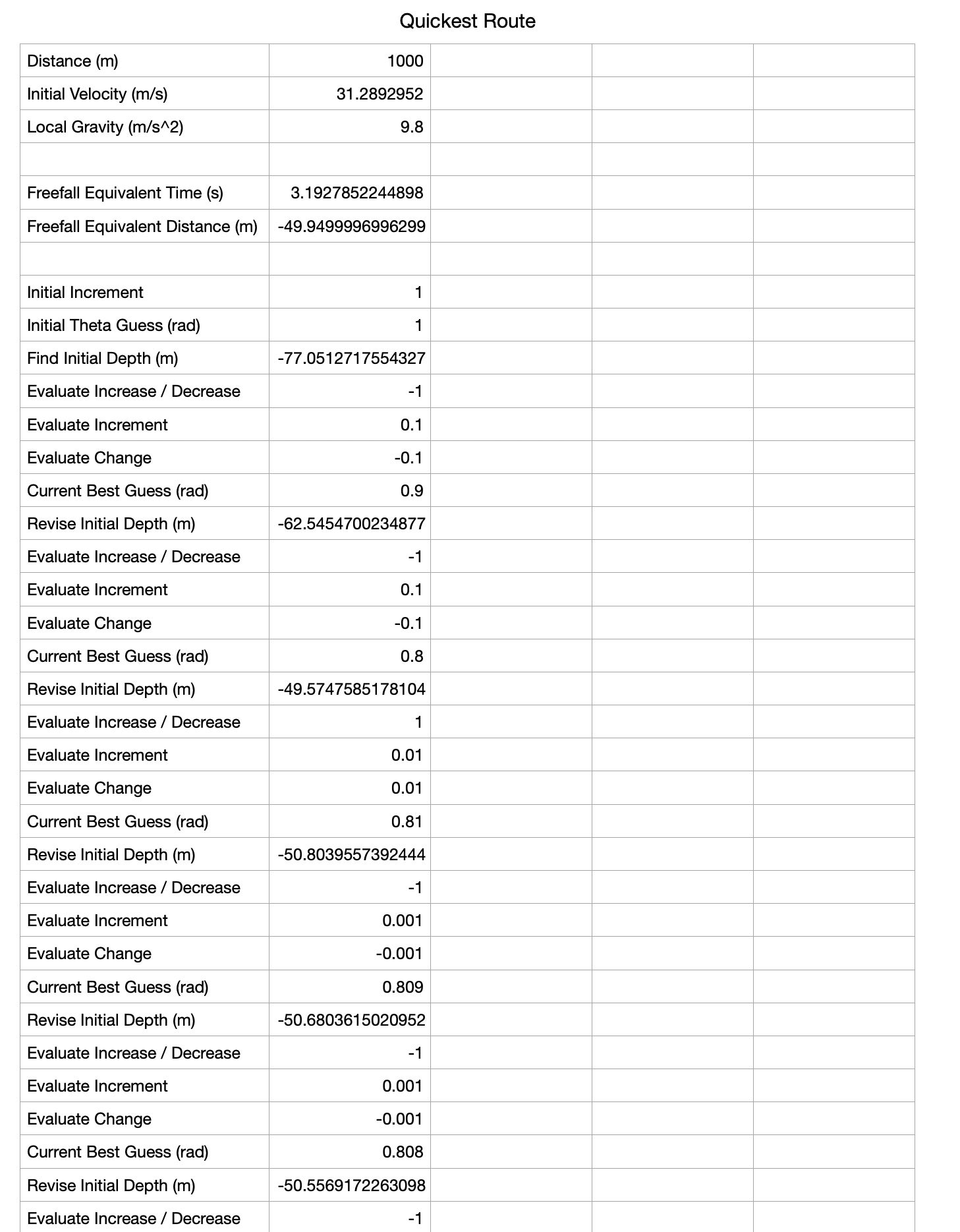
Suppose the stations are 1km apart and within the station my vehicle can accelerate to 70mph (31.29m/s)...
It takes 3.19286s to reach 31.29m/s accelerating at 9.8m/s^2 (1g), which is equivalent to a vacuum freefall to a depth of 49.95m.
A=-49.95m
B=1000m
A=-(B/2(pi-t+sin(t)))(1-cos(t))
t=0.8030657
2pi-0.8030657=5.480119607179586476925
r=B/(2(pi-t+sin(t)))
r=163.5047270224771254028
time_whole_cycloid_seconds=2*pi*sqrt(r/g) = 25.66445149976236809604... seconds
dtime=sqrt(r/g)*dtheta = 3.280221687114986200164 seconds
19.10400812553239569571 seconds = 25.66445149976236809604-3.280221687114986200164-3.280221687114986200164
1000m / 19.104s = 52.345m/s avg horizontal effective velocity
1000m / 31.29m/s = 31.95 seconds
19.104s seconds / 31.95 seconds = 59.79%
31.95 seconds / 19.104s seconds = 167.24%
The 1km horizontal travel time with 70mph initial velocity with a flat track is 67.2% longer (31.9 seconds) than with an optimal curved track (19.1 seconds). The average effective horizontal velocity within the optimal curved track is 117.08mph, equivalent to an instantaneous 47.08mph horizontal acceleration upon entering the track.
Any help rearranging the equation would be appreciated, thanks in advance for any help.
I’ve been struggling to rearrange this formula which has to do with the geometry of a cycloid.
I want to rearrange this formula to solve for t but find it very difficult:
A=-(B/2(pi-t+sin(t)))(1-cos(t))
It has to do with the Brachistochrone problem of finding the ramp/path of quickest descent with no friction and only gravity, but with the added twist of having an initial velocity and the 2 points are horizontal to each other.
The way I’ve solved it so far is as follows:
Suppose the stations are 1km apart and within the station my vehicle can accelerate to 70mph (31.29m/s)...
It takes 3.19286s to reach 31.29m/s accelerating at 9.8m/s^2 (1g), which is equivalent to a vacuum freefall to a depth of 49.95m.
A=-49.95m
B=1000m
A=-(B/2(pi-t+sin(t)))(1-cos(t))
t=0.8030657
2pi-0.8030657=5.480119607179586476925
r=B/(2(pi-t+sin(t)))
r=163.5047270224771254028
time_whole_cycloid_seconds=2*pi*sqrt(r/g) = 25.66445149976236809604... seconds
dtime=sqrt(r/g)*dtheta = 3.280221687114986200164 seconds
19.10400812553239569571 seconds = 25.66445149976236809604-3.280221687114986200164-3.280221687114986200164
1000m / 19.104s = 52.345m/s avg horizontal effective velocity
1000m / 31.29m/s = 31.95 seconds
19.104s seconds / 31.95 seconds = 59.79%
31.95 seconds / 19.104s seconds = 167.24%
The 1km horizontal travel time with 70mph initial velocity with a flat track is 67.2% longer (31.9 seconds) than with an optimal curved track (19.1 seconds). The average effective horizontal velocity within the optimal curved track is 117.08mph, equivalent to an instantaneous 47.08mph horizontal acceleration upon entering the track.
Any help rearranging the equation would be appreciated, thanks in advance for any help.