Rational Function Help

[alz92]

I have a type of problem that i need some major help on. I am not getting at all how to do this. the problem is....


It costs a company $30,000 to begin production of a good, plus $3 for every unit of the good produced. Let x be the number of units produced by the company.

a.) Find a formula for C(x), the total cost for the production of x units of the good.
b.) Find a formula for the company's average cost per unit, a(x).
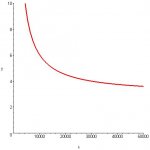
c.) Graph y=a(x) for 0< x <(or equal to) 50,000, 0<(or equal to) y <(or equal to)10.
d.) Explain in economic terms why the graph of a has the long-run behavior that it does.
e.) Explain in economic terms why the graph of a has the vertical asymptote that it does.
f.) Find a formula for a^-1(y). give an economic interpretation of a^-1(y).
g.) The company makes a profit if the average cost of its good is less than $5 per unit. Find the minimum number of units the company can produce and make a profit.



Steps to find the answers will be greatly appreciated.

Thanks,
alz92

 

[BigGlenntheHeavy]

\(\displaystyle x \ = \ the \ number \ of \ units \ produced \ (or \ sold)\)

\(\displaystyle p \ = \ price \ per \ unit\)

\(\displaystyle C \ is \ the \ total \ cost \ producing \ x \ units\)

\(\displaystyle a) Hence, \ C(x) \ = \ 30,000+3x\)

\(\displaystyle \overline C \ is \ the \ average \ cost \ per \ unit. \ \overline C \ = \ \frac{C}{x}\)

\(\displaystyle b) \ Therefore, \ a(x) \ = \ \overline C \ = \ \frac{30,000+3x}{x}\)

\(\displaystyle c) \ See \ graph\)

[attachment=0:1pj60uht]bbb.jpg[/attachment:1pj60uht]

\(\displaystyle d) \ \lim_{x\to\infty}a(x) \ = \ 3\)

\(\displaystyle e) \ At \ x \ = \ 0 \ we \ have \ a \ vertical \ asymptote \ as \ division \ by \ zero \ is \ undefined.\)

 

[alz92]

Thank you so much that helped a whole lot. now for part f.) i have to find the inverse of a(x). not sure on how to come about getting the inverse