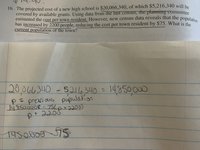I’ve been stuck on this word problem for over a week and am unsure how to format the equation or if I need to make multiple equations. The wording is very confusing for me, so I’d like help understanding how to write the equation they want and then how to solve it as I couldn’t find any similar examples in my text book right now. I think I need to find what the cost per person was before? And then what it is now to find the current population? But I’m unsure.
Rational Equation Help
- Thread starter kathrynk
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,749
What you've done is to leap to a solution (an expression) without writing an equation! But you did well in starting by defining a variable carefully. Note, however, that your variable is not what you are asked for, so you'll have to do some work after solving for p. You could make a different choice of variable to avoid that.
The equation you write will state the goal, without yet solving anything.
So first look at what has to be true: the (net) cost per resident has to decrease by $75. That implies you need to write two expressions, in terms of your variable, for the cost per resident, before and after (just as you suggested).
Then your equation will say [new cost per resident] = [old cost per resident] - 75.
Then you can solve that equation.
Give that a try,
I’m sorry, I need more help understanding how to write that to get something that makes sense. My book gives a lot of different equations for different situations and I don’t know which one to use because none of them look like they apply. (Also I have discalculia from adhd so I’m sorry if this seems like a simple fix. It just isn’t obvious to me)
Attachments
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
You have two unknowns. One is the original population (or if you prefer, the current population) and the other unknown is how much it will cost each person before the additional people are including.
Can you try to write two equations? Hint: write one for the original population and one for the new updated population.
Please post back.
Can you try to write two equations? Hint: write one for the original population and one for the new updated population.
Please post back.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,749
You got all the basic details, but had trouble putting them together. Often it's a good thing to use more variables than you need, but your new variable c is probably getting in your way. I would stick with the variable you chose, p = previous population.
The past cost per person is, as you wrote, 14,850,000/p.
The new cost per person is, as you also wrote, 14,850,000/(p+2200).
So the equation I suggested is that the latter is $75 less than the former:
[new cost per resident] = [old cost per resident] - 75
[14,850,000/(p+2200)] = [14,850,000/p] - 75
(There are other ways you could write it.)
Now, can you make a start at solving this?
Word problems teach you how to actually use algebra. They can not be reduced to formulas because reality cannot be reduced to a formula. But there is a method that I like.
Personally, I like to start by determining what is unknown. So I would start with the fact that there are FOUR numbers that are unknown. Let's assign a separate symbol to each and write it down so we know what we are talking about.
[MATH]p_{o} = \text {population according to old census.}[/MATH]
[MATH]p_{e} = \text {estimated population now.}[/MATH]
[MATH]c_{o} = \text {cost per person if old census is correct.}[/MATH]
[MATH]c_{e} = \text {cost per person if current estimate is correct.}[/MATH]
Next, we know that four equations may be sufficient to find four unknowns. So that tells us what we need to look for. What do we know is equal to what?
[MATH]p_e = p_o + 2200.[/MATH] Easy. You are told that.
[MATH]c_o = \dfrac{20,066,340 - 5,216,340}{p_o} = \dfrac{14,850,000}{p_o}.[/MATH]
By definition of what "per" means.
[MATH]c_e = \dfrac{14,850,000}{p_e}[/MATH]
Also by definition of what "per" means.
[MATH]c_o - c_e = 75.[/MATH] That is clearly implied, but not explicitly stated.
This last is the only one that requires even a bit of thought.
Now the general way to solve simultaneous equations is by substitution.
[MATH]p_e = p_o + 2200 \implies c_e = \dfrac{14,850,000}{p_o + 2200},[/MATH] Right?
Therefore
[MATH]c_e - c_o = 75 \implies \\ \dfrac{14,850,000}{p_o + 2200} - \dfrac{14,850,000}{p_o} = 75.[/MATH]You have an equation in one unknown. Now it is mechanical to solve it.
Personally, I like to start by determining what is unknown. So I would start with the fact that there are FOUR numbers that are unknown. Let's assign a separate symbol to each and write it down so we know what we are talking about.
[MATH]p_{o} = \text {population according to old census.}[/MATH]
[MATH]p_{e} = \text {estimated population now.}[/MATH]
[MATH]c_{o} = \text {cost per person if old census is correct.}[/MATH]
[MATH]c_{e} = \text {cost per person if current estimate is correct.}[/MATH]
Next, we know that four equations may be sufficient to find four unknowns. So that tells us what we need to look for. What do we know is equal to what?
[MATH]p_e = p_o + 2200.[/MATH] Easy. You are told that.
[MATH]c_o = \dfrac{20,066,340 - 5,216,340}{p_o} = \dfrac{14,850,000}{p_o}.[/MATH]
By definition of what "per" means.
[MATH]c_e = \dfrac{14,850,000}{p_e}[/MATH]
Also by definition of what "per" means.
[MATH]c_o - c_e = 75.[/MATH] That is clearly implied, but not explicitly stated.
This last is the only one that requires even a bit of thought.
Now the general way to solve simultaneous equations is by substitution.
[MATH]p_e = p_o + 2200 \implies c_e = \dfrac{14,850,000}{p_o + 2200},[/MATH] Right?
Therefore
[MATH]c_e - c_o = 75 \implies \\ \dfrac{14,850,000}{p_o + 2200} - \dfrac{14,850,000}{p_o} = 75.[/MATH]You have an equation in one unknown. Now it is mechanical to solve it.
okay I know there is an equation in the book similar to that so I will try following the steps like it shows for solving and get back to you all with my work
Okay so i followed Dr Peterson’s advice with the equation and I’m now to p^2 + 2200p = 435600000 and then p^2 + 2200p - 435600000 = 0
And then I got stuck again. I’m using the Photomath app to help me and it wants me to make 2200p a difference by writing 22000p - 19800p in its place but I don’t understand why?
D
Deleted member 4993
Guest
Because that is a quadratic equation!
What methods have you learned to solve a quadratic equation?
Well. I’ve “done them” but I’m very bad at retaining information on like the name of equations and the steps to solve them. But I will look it up in the glossary of my book and try to find an example. Like I know to get rid of the exponent I could do p(p + 2200) but I forgot how to do this with an additional number involved.
Okay I think the kind of way the book and the way I’d be most comfortable doing it is factoring but I often make very silly mistakes when doing it bc there are a lot of rules especially with positive and negative so I get messed up easily
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,749
There are different ways to solve it. This particular method might be called factoring by ac-grouping, or decomposition and grouping. It would be nice if the software at least gave you a hint about that.
But you should use whatever method you have learned and want to try; that can include the quadratic formula, which might be quicker for such big numbers. And if you're trying to follow what someone else says, and you can't ask them what they're doing (that's the disadvantage of software!), just back up and try to recall what you've learned.
Okay I think I got it? And why photomath wanted me to use those numbers? Bc 435600000 can be divided by them so they can be used in the factoring part but I think the way it explained it got me confused. So it’s (p + 22000)(p - 19800) = 0. So the only work I’ll have to do is like. Figuring out if p is the previous population or the cost per person.... so may need help there
I got it! I checked my work, just to see like. Current vs previous population and the cost per person and it was in fact $75 less. Thank you all for your help