This is an interesting problem! If, like me, you have absolutely no familiarity with this sort of situation, and you
have to start from scratch--with no template at all to guide you--to devise strategy and tactics, it is one of those
taxing but invigorating experiences. I strongly encourage anyone who enjoys mathematical just-hands-and-
feet-and-no-equipment rock climbing to stop reading now and go off and take a crack at solving it.
Here's my solution--I checked it and I'm pretty certain (though only my dog considers me infallible):
First, don't take the terms "beach ball" and "tennis ball" literally--I don't know if they're in the correct ratio, not
having a beach ball handy I can't confirm or deny. Also, whatever the size of the larger ball, there's always a
smaller (by the same ratio) ball that will satisfy the conditions,i.e. both balls are tangent to the 2 walls and the
floor and to each other. By the way, this solution I'm presenting will give highlights, since it's too complicated to
lay out every excruciating detail--not to mention some ugly false steps of mine! Visualization is required, and
varying your viewpoint. It's helpful to take an aerial view as well as 2 different street level views.
Second, let me express the key strategy. If you think about it, you'll realize that there are an infinite number of
smaller balls of various sizes that will fit into the space between the larger ball and the corner and be tangent to
the larger; however only one will also be tangent to the walls and floor. Thus, I decided to start out by
establishing the tangency to the walls and floor of the smaller ball. Eventually, we're going to shift viewpoints to
a line from the center of the larger ball to the corner.(Incidentally, I'm calling the length of the radius of the
larger ball "one", so that the distance from the center of that ball to the corner is SQRT(2) (the larger ball is
tangent to both walls, so the distance from the center to each wall is one, and thus you have a 45 degree angle,
etc.). But for the moment we have to adopt a different perspective. Imagine you're lying on the floor, outside
the room, looking through the wall. Directly in front of you are the two balls, to the right is the corner, and
you're looking directly toward the opposite wall. So the radius of the smaller ball is the perpendicular distance
from the center to the wall to the right, and the perpendicular distance to the wall in front of you that you are
looking through (and to the floor). That we call "r". Now we have to translate that distance to the SQRT(2) line
that we will be working with for the rest of the problem. Fortunately, it's simple because we have a right
triangle with a 45 degree angle, so the distance from the corner to the center of the smaller ball on the SQRT(2)
line is SQRT(2)*r. Since we're going to be measuring from the other end of this line, let's express it the other
way, as SQRT(2)-SQRT(2)*r.
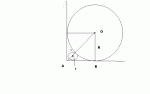
Now I must be very precise. For all the remaining analysis and calculations I'm going to be using the following
perspective. First, at this point we can use 2 dimensions, a big circle for the larger ball, a little for the smaller,
in the plane that has the center of both balls and the corner. Why can we do this? Since the balls are
symmetrical, the point of tangency must occur in this plane. Further, it will occur on the lower right quadrant of
the big circle, and the upper left quadrant of the small. For this reason the line that will be the x-axis in this
analysis goes under both circles--the floor level in other words--which presents some difficulties with
equations, but more on that momentarily.
Now, point 0 on the x-axis is a point directly below the center of the large circle and, as I just said, the action will
take place somewhere on the lower right quadrant, instead of what usually happens with circles, namely the
upper right quadrant. Therefore, we have to modify the equation so that the bottommost point on the circle, on
the floor at x=0 yields y=0 instead of -1. Thus the function for the y-values of the larger circle is y=1-(1-x^2)^.5,
with one being the radius.
Now here's a crucial idea. The point of tangency will occur when two things happen:1)The equation for the big
circle at some unknown x will produce the same exact y as the equation for the smaller circle at the same x. 2)
The two derivatives of the two circle equations will yield identical slopes for that (x,y) just mentioned.
We already have the equation of the big circle. The one for the small takes a little doing. The expression that
will appear in the x-position isn't simply x, because the center of this circle is in a different place--and the y
value produced by the equation must also reflect our actual baseline, the floor. So we create a term that serves
the normal role of x, expressing the distance from the smaller circle's center: (SQRT(2)-SQRT(2)*r-x). So, taking
into account that we're dealing with the upper left quadrant of the small circle for the point of tangency, the
equation is: y(small circle)= (r^2-(SQRT(2)-SQRT(2)*r-x)^2)^.5 + r. The r at the end is because the equation
without it just gives the height of y above the center line, not above the floor, which is our actual baseline. So
the first equation we have seeks a matching y value for some value of x.
1-(1-x^2)^.5=(r^2-(SQRT(2)-SQRT(2)*r-x)^2)^.5 + r.
Now we need to have matching slopes--after all, you can have a point in common but it can simply be an
intersection--we don't want that. Anyway, we have 2 unknowns, so we must have a second equation. This will
be the derivatives of each side of the first equation. We get the derivatives and set them equal to each other:
x*(1-x^2)^-.5=.5*(r^2-2+4r+2*SQRT(2)*x-2r^2-2*SQRT(2)*r*x-x^2)^-.5*(2*SQRT(2)-2*SQRT(2)*r-2x) Now
add our first equation
1-(1-x^2)^.5=(r^2-(SQRT(2)-SQRT(2)*r-x)^2)^.5 + r and solve simultaneously for r and x. You get:
r=.26794919243112 x=.81649658092775 The ratio of radii of the big to little ball is 3.73205. The slope at
the point of tangency, identical from both derivatives, is 1.414213, or the SQRT(2). If you go back to the
beginning and plug the values in , everything checks out perfectly.
Now, I have a suspicion that's gnawing at me with increasing insistence--somebody will post an elegant 2
sentence, largely geometrical solution based on that provocative SQRT(2) slope, with the majestic simplicity of
Archimedes' calculus-2-millenia-ahead-of-its-time derivation of the equation for the volume of a sphere,
rendering all my labor superfluous. Crowds will gather in the street to mock me for the clumsiness of my
solution. It'll be cruel of the poster to initiate all this, but in the interests of truth, beauty, etc., let him proceed.