Rate Question...Anoter Issue

[stevenrand]

My work for what I have so far is below the image...
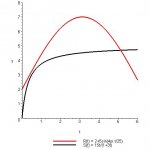
[attachment=0:20rn5o2v]fmhq.jpg[/attachment:20rn5o2v]
For (A) I have 31.186 cubic yards beause I did the integral of R(t) from zero to six.
(B) This is just a guess...I am not sure how to do this: Y(t) = 2500 + S(t) - R(t)???
(C) I think I need to plug in 4 for t (in my equation from part B) but I do not feel like B is right so I didn't do it.
(D) Just based on a graph I thought it may be at 4.5 hours?

 

[galactus]

part a: \(\displaystyle \int_{0}^{6}[2+5sin(\frac{4{\pi}t}{25})]dt\)

b: Let A(t) be the amount of sand at time t. Then, we have

\(\displaystyle A(t)=2500+\int_{0}^{t}\left[\frac{15x}{1+3x}-(2+5sin(\frac{4{\pi}t}{25}))\right]dt\)

we use x as a dummy variable so we do not have a dependent variable.

c. A'(t)=S(t)-R(t)

d. Set A'(t)=0 and solve for t. i.e. when S(t)-R(t)=0

It is a little more than 4.5 hours.

 

[BigGlenntheHeavy]

\(\displaystyle Given: \ R(t) \ = \ 2+5sin(4\pi t/25), \ S(t) \ = \ \frac{15t}{1+3t}, \ Y(0) \ = \ 2500 \ cu. \ yds., \ and \ 0 \ \le \ t \ \le \ 6.\)

\(\displaystyle a) \ \int_{0}^{6}[2+5sin(4\pi t/25)]dt \ \dot= \ 31.8159 \ cu. \ yds. \ of \ sand \ will \ be \ removed \ from \ the\)

\(\displaystyle beach \ in \ a \ 6 \ hour \ period.\)

\(\displaystyle b) \ Y(t) \ = \ 2500+\int_{0}^{t}\bigg[\frac{15x}{1+3x}-(2+5sin(4\pi x/25))\bigg]dx\)

\(\displaystyle c) \ Y'(4) \ \dot= \ -1.90875 \ cu. \ yds. \ per \ hour. \ In \ other \ words, \ at \ the \ exact \ t \ = \ 4 \ hrs., \ the\)

\(\displaystyle beach \ is \ losing \ 1.90875 \ cu. \ yds. \ of \ sand.\)

\(\displaystyle d) \ Y'(t) \ = \ \frac{15t}{1+3t}-(2+5sin(4\pi t/25) \ = \ 0, \ t \ \dot= \ 5.1178\)

\(\displaystyle Therefore \ at \ about \ 5.1178 \ hours, \ there \ is \ about \ 2492.3694 \ cu. \ yds. \ of \ sand \ on \ the \ beach, \\)

\(\displaystyle the \ sea \ having \ claimed \ about \ 7.6306 \ cu. \ yds.\)

\(\displaystyle See \ graph.\)

[attachment=0:124uklfv]ghi.jpg[/attachment:124uklfv]

 

[stevenrand]

I see. So part B I would leave the integral alone in the expression...okay that makes sense. Now if in the expression I had the integrated result of that, would I just have to find the value of C (if that makes sense)?

And as for part C, that is simply plugging in my value of t=4 into the expression give in part B? Wow; that seems almost too simple.
Also for part C: Is that just the amount of sand on the beach? In the question it asks for the rate at which the total amount of sand on the beach is changing. So is that an actual rate or just the amount?

 

[BigGlenntheHeavy]

Note: my mistake, I re-edited c, see above.

 

[stevenrand]

Oh, okay. Now C makes more sense. One more question:

For part D:
When I set the equation equal to 0 I then solve for t yes? I am not sure how to do that by hand so I used the calculator and got roughly -7.646....Do I take this value and plug it into the integral from part B to get the 5.118? I am not sure what is going on there. Sorry for all the trouble, I just need to get my head wrapped around this.

 

[BigGlenntheHeavy]

\(\displaystyle This \ is \ (d) \ a \ min/max \ problem, \ and \ if \ you \ have \ come \ this \ far, \ you \ shouldn't \ have \ a \ problem\)

\(\displaystyle \ here, \ however \ you \ question \ leaves \ a \ little \ to \ be \ desire.\)

\(\displaystyle Basically \ set \ the \ slope \ = \ to \ zero \ and \ solve \ for \ the \ variable, \ usually \ x \ or \ t, \ then \ plugged \ you\)

\(\displaystyle answer \ into \ the \ original \ function \ to \ get \ the \ other \ point. \ You \ should \ know \ this.\)

\(\displaystyle Your \ domain \ is \ given \ as \ 0 \ \le \ t \ \le \ 6, \ so \ what's \ with \ the \ t \ = \ -7.646?\)