okay, i don't usually have any trouble with this but i just cant seem to make my work match what my calculator says the answer is. So here we go.
Find the first derivative:
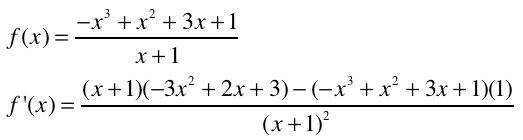
then, i try to simplify:
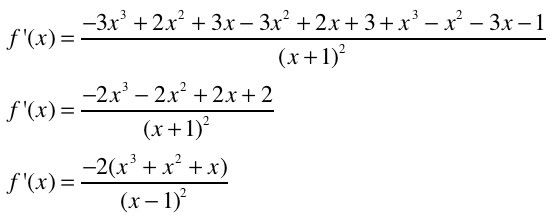
(there is a typo in the above image, it's supposed to be a negative x on the top, and a positive 1 on the bottom of the last equation, obviously)
the answer my TI-89 calculator spits out when i use the differentiate function is
f'(x)=-2(x-1)
and i can't get it. please tell me where i screwed up, or if im just out of it and not thinking of some simple simplification type of thing to get from where i am to the "correct" answer.
i'd also like to know what some of you use to type math problems for this forum, ive been using a program called MathType for Mac, but the trial is about up. Its also quite a pain to type it, capture it as an image with grab, convert from tiff to jpg, upload to photobucket, and then add the link. is there any easier way?
Find the first derivative:
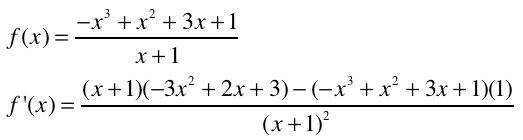
then, i try to simplify:
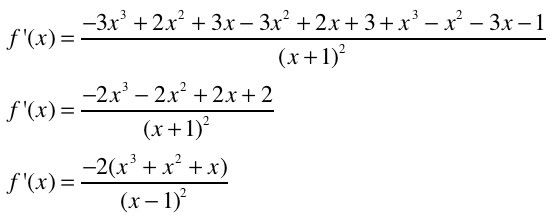
(there is a typo in the above image, it's supposed to be a negative x on the top, and a positive 1 on the bottom of the last equation, obviously)
the answer my TI-89 calculator spits out when i use the differentiate function is
f'(x)=-2(x-1)
and i can't get it. please tell me where i screwed up, or if im just out of it and not thinking of some simple simplification type of thing to get from where i am to the "correct" answer.
i'd also like to know what some of you use to type math problems for this forum, ive been using a program called MathType for Mac, but the trial is about up. Its also quite a pain to type it, capture it as an image with grab, convert from tiff to jpg, upload to photobucket, and then add the link. is there any easier way?
