Quick question - isosceles triangle

[Jm23]

Guys quick question... what is the proof behind two radii and a chord forming isosceles triangle? Every textbook states this fact but what if the chord is equal to the radius - would that not make it equilateral triangle?

 

[Harry_the_cat]

An equilateral triangle is an isosceles triangle in my opinion, although others may disagree. Just like a square is a rectangle.

 

[pka]

Guys quick question... what is the proof behind two radii and a chord forming isosceles triangle? Every textbook states this fact but what if the chord is equal to the radius - would that not make it equilateral triangle?

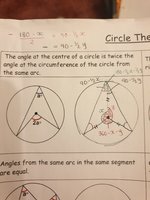
Your terminology is a bit off. The radius of a circle is a number. A line segment having the centre of the circle as one endpoint and a point of the circle as the other endpoint is a radial segment. The length of any radial segment is the radius of the circle. Now if a triangle has two sides that are radial segments of the same circle then by definition that triangle is isosceles. And of course, if the third side has length equal to the radius of the circle the that triangle is equilateral.

 

[Jm23]

See number 2.. The reason I ask is if the chord is equal to the radial segment, then this book is technically incorrect..

 

[Jm23]

This proof can therefore also be questioned.

 

[Dr.Peterson]

This is precisely why, in mathematics, we generally use "inclusive" definitions, as illustrated in post #2. An equilateral triangle is a special case of isosceles triangle; the latter includes the former. That is, any equilateral triangle can also be called isosceles. See here:

Isosceles Triangle -- from Wolfram MathWorld

An isosceles triangle is a triangle with (at least) two equal sides. In the figure above, the two equal sides have length b and the remaining side has length a. This property is equivalent to two angles of the triangle being equal. An isosceles triangle therefore has both two equal sides and two...

mathworld.wolfram.com

If we didn't define terms this way, then we would have to state many theorems in complicated ways, such as, "two non-collinear radii of a circle, together with the chord joining their endpoints, form an isosceles or equilateral triangle".

The same is true of quadrilaterals: a square is a special rectangle, which is a special parallelogram, which is a special quadrilateral. So a theorem about parallelograms applies in particular to squares. We can just say, "Opposite angles of a parallelogram are congruent", rather than "Opposite angles of a parallelogram, rhombus, rectangle, or square are congruent".

[You don't need to stop using "radius" to mean the segment. Use your book's or teacher's terms; this is a long-established usage. Check any dictionary.]

 

[Jm23]

This is precisely why, in mathematics, we generally use "inclusive" definitions, as illustrated in post #2. An equilateral triangle is a special case of isosceles triangle; the latter includes the former. That is, any equilateral triangle can also be called isosceles. See here:

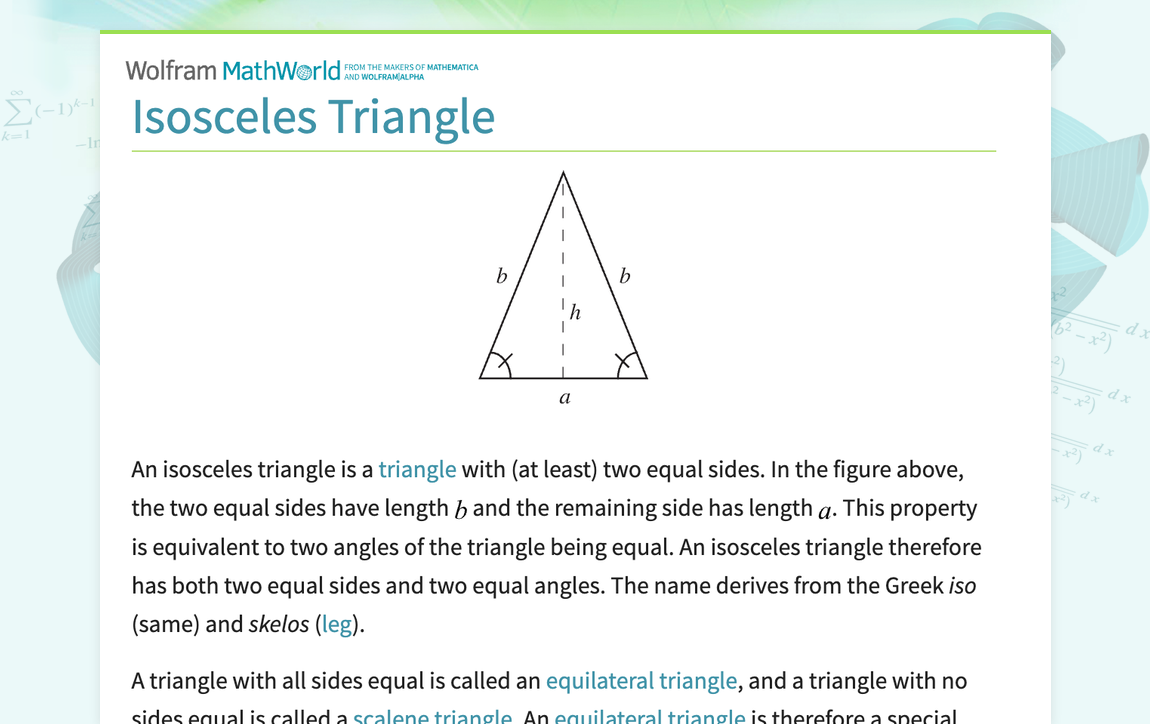
Isosceles Triangle -- from Wolfram MathWorld

An isosceles triangle is a triangle with (at least) two equal sides. In the figure above, the two equal sides have length b and the remaining side has length a. This property is equivalent to two angles of the triangle being equal. An isosceles triangle therefore has both two equal sides and two...

mathworld.wolfram.com

If we didn't define terms this way, then we would have to state many theorems in complicated ways, such as, "two non-collinear radii of a circle, together with the chord joining their endpoints, form an isosceles or equilateral triangle".

The same is true of quadrilaterals: a square is a special rectangle, which is a special parallelogram, which is a special quadrilateral. So a theorem about parallelograms applies in particular to squares. We can just say, "Opposite angles of a parallelogram are congruent", rather than "Opposite angles of a parallelogram, rhombus, rectangle, or square are congruent".

[You don't need to stop using "radius" to mean the segment. Use your book's or teacher's terms; this is a long-established usage. Check any dictionary.]

THANK YOU Dr Peterson and all who contributed.. Makes sense now.

 

[pka]

See number 2.. The reason I ask is if the chord is equal to the radial segment, then this book is technically incorrect..

Your image is sideways, so I cannot read it.
What does your text say? It is possible for a triangle to have the centre and two points of the circle as vertices. In such a triangle if the side that is a cord has length equal to the radius then the triangle is equilateral.