I'm confused a bit, by these problems:
1)It says to simplify:

I get this,
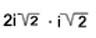
Hope fully, it all simplifies to this \(\displaystyle 2i^2\) * \(\displaystyle 2\)
Then I get -2*2=-4,
I'm not sure about this, but am I doing something wrong?
Also, theres another problem:
10*sqroot(-50), I get 50i*sqroot(2)
1)It says to simplify:

I get this,
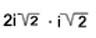
Hope fully, it all simplifies to this \(\displaystyle 2i^2\) * \(\displaystyle 2\)
Then I get -2*2=-4,
I'm not sure about this, but am I doing something wrong?
Also, theres another problem:
10*sqroot(-50), I get 50i*sqroot(2)
