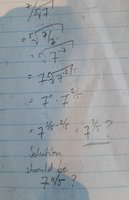You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Question about changing roots to powers
- Thread starter e.spyck
- Start date
Cubist
Senior Member
- Joined
- Oct 29, 2019
- Messages
- 1,699
It seems that the question is asking you to show the following...
[math] \frac{7}{\sqrt[5]{7}} = 7^{\frac{4}{5}} [/math]
But on your first 2 lines you imply...
[math] \frac{7}{\sqrt[5]{7}}=\sqrt[5]{\frac{\color{red}7\color{black}}{7}}[/math] but this isn't correct.
Think about the numerator only, what value of "x" would satisfy...
[math] 7=\sqrt[5]{7^x}[/math]
EDIT: When you find x, then the following progression would be correct...
[math] \frac{7}{\sqrt[5]{7}}= \frac{\sqrt[5]{7^x}}{\sqrt[5]{7}} = \sqrt[5]{\frac{7^x}{7}}[/math]... and continue
[math] \frac{7}{\sqrt[5]{7}} = 7^{\frac{4}{5}} [/math]
But on your first 2 lines you imply...
[math] \frac{7}{\sqrt[5]{7}}=\sqrt[5]{\frac{\color{red}7\color{black}}{7}}[/math] but this isn't correct.
Think about the numerator only, what value of "x" would satisfy...
[math] 7=\sqrt[5]{7^x}[/math]
EDIT: When you find x, then the following progression would be correct...
[math] \frac{7}{\sqrt[5]{7}}= \frac{\sqrt[5]{7^x}}{\sqrt[5]{7}} = \sqrt[5]{\frac{7^x}{7}}[/math]... and continue
Last edited:
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,760
I would do it the other way around:
\(\displaystyle \frac{7}{\sqrt[5]{7}}= \frac{7^1}{7^{1/5}}= 7^{1-1/5}= 7^{5/5- 1/5}\).
\(\displaystyle \sqrt[n]{a}= a^{1/n}\) and \(\displaystyle \frac{1}{a^n}= a^{-n}\).
\(\displaystyle \frac{7}{\sqrt[5]{7}}= \frac{7^1}{7^{1/5}}= 7^{1-1/5}= 7^{5/5- 1/5}\).
\(\displaystyle \sqrt[n]{a}= a^{1/n}\) and \(\displaystyle \frac{1}{a^n}= a^{-n}\).