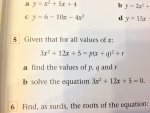Quadratic functions

[aurkhan]

Can somebody please help me with this A level maths question from chapter 2, page 25 of the edexcel C1 textbook:


Given that for all values of x:

3x^2 + 12x + 5 = p(x+q)^2 + r

Find the values of p, q and r?


Can somebody please tell me what principle to follow to find the values of p, q and r for above question ? According to the answers, p=3 and q=2 and r= - 7. But how do you work this out? Can somebody please show all the steps in the algebra working for this so I can understand how to reach the solution


Thank you


Regards


Ahsan
P.s any maths tutors in central London interested in providing tuition for A level maths? Please call me 07557-964443 or email aur_khan@hotmail.com

 

[Bob Brown MSEE]

3x^2 + 12x + 5 = p(x+q)^2 + r

1) Expand the RHS (right hand side)
2) Equate terms corresponding powers of x from the LHS

eg: 3x^2 = px^2
p=3

This is justified because polynomial expressions are unique

 

[aurkhan]

Dear bob,
thank you but if u expand the RHS u get the following:

3x^2 + 12x + 5 = px^2 + pq^2 + 2pqx + r

I understand from your answer and logic that 3x^2 = px^2 and thus p=3

but what about pq^2 ? I have to plug in the values of p which we just found out and hence we get:

3x^2 + 3q^2 + 2(3)qx + r
3x^2 + 3q^2 + 6qx + r

We assume 2pqx from RHS is equal to 12x from LHS right?

Since we know p=3 so we insert that

2(3)qx= 12x
6qx=12x
hence we assume that 6q=12 and therefore q=2

now that we know both p and q we insert these back into main eq
Hence:

3x^2 + 3(2)^2 + 6(2)x + r
3x^2 + 3(4) + 12x + r
3x^2 + 12 + 12x + r

and to get this equal to the LHS we know that r must be -7 as we have to subtract this from 12 in order to get the LHS digit of 5

is this all correct logic and working?

 

[Deleted member 4993]

Dear bob,
thank you but if u expand the RHS u get the following:

3x^2 + 12x + 5 = px^2 + pq^2 + 2pqx + r

I understand from your answer and logic that 3x^2 = px^2 and thus p=3

but what about pq^2 ? I have to plug in the values of p which we just found out and hence we get:

3x^2 + 3q^2 + 2(3)qx + r
3x^2 + 3q^2 + 6qx + r

We assume 2pqx from RHS is equal to 12x from LHS right?

Since we know p=3 so we insert that

2(3)qx= 12x
6qx=12x
hence we assume that 6q=12 and therefore q=2

now that we know both p and q we insert these back into main eq
Hence:

3x^2 + 3(2)^2 + 6(2)x + r
3x^2 + 3(4) + 12x + r
3x^2 + 12 + 12x + r

and to get this equal to the LHS we know that r must be -7 as we have to subtract this from 12 in order to get the LHS digit of 5

is this all correct logic and working?

Yes your work is correct.

To summerize:

3x² + 12x + 5 = p(x+q)² + r

3x² + 12x + 5 = p(x² + q² + 2qx) + r

Equating coefficients of x², x¹ & x⁰ - we get

3 = p

12 = 2pq → q = 2

5 = pq² + r → r = 5 - 12 → r = - 7

 

[aurkhan]

Dear khan sb
thank u it's perfectly clear now.
thats same explanation my professor has replied with by email.
are you in London ?
I am looking for a private tutor and obviously willing to pay for it.
maths and physics both.
and a civil engineer to tutor me for civil engineering degree also if possible eg fluids, soils, structures, design, geomatics, mechanics

my contacts are:
Ahsan khan
07557-964443
aur_khan@hotmail.com

 

[Deleted member 4993]

Dear khan sb
thank u it's perfectly clear now.
thats same explanation my professor has replied with by email.
are you in London ?
I am looking for a private tutor and obviously willing to pay for it.
maths and physics both.
and a civil engineer to tutor me for civil engineering degree also if possible eg fluids, soils, structures, design, geomatics, mechanics

my contacts are:
Ahsan khan
07557-964443
aur_khan@hotmail.com

I live in USA. Good luck with your search for a tutor...