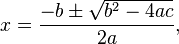airbornewife29
New member
- Joined
- Jul 23, 2010
- Messages
- 5
I need some help. Can anyone help me? We are doing quadratic equations. I am lost.
First problem; q(x)= 2x^2 + 3x - 1
The other problem;
Question:
To answer this question: Solve (x-1)^2=-49
Suppose your classmate wrote the first step of the solution as:
Take square root
x – 1 = 7 or x - 1 = -7
We now add 1 to each side of equations to solve for x.
x = 8 or x = -6
This is not correct since neither answer checks in the original equation. Can you correct this error? Please explain your thinking in simple language.
First problem; q(x)= 2x^2 + 3x - 1
The other problem;
Question:
To answer this question: Solve (x-1)^2=-49
Suppose your classmate wrote the first step of the solution as:
Take square root
x – 1 = 7 or x - 1 = -7
We now add 1 to each side of equations to solve for x.
x = 8 or x = -6
This is not correct since neither answer checks in the original equation. Can you correct this error? Please explain your thinking in simple language.