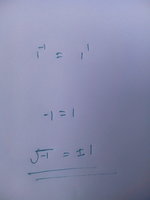Proving square root of -1(i) is =1

[Vara1803]

View the attachment

 

[pka]

\(-1(\bf{i})=-{i}\)=\(\exp \left( {\dfrac{{ - \pi i}}{2}} \right)\)
So the square roots are \(\exp \left( {\dfrac{{ - \pi i}}{4}} \right)~\&~\exp \left( {\dfrac{{ 3 \pi i}}{4}} \right)\)
SEE HERE Scroll to the end of the page.

 

[Dr.Peterson]

You are wrongly assuming that the square root has a single value.

This is absolutely not true for complex numbers; but you should know even from solving equations in real numbers that when you take the square root of both sides, you must use the [MATH]\pm[/MATH] sign, because there are two square roots.

 

[pka]

You are wrongly assuming that the square root has a single value.
This is absolutely not true for complex numbers; but you should know even from solving equations in real numbers that when you take the square root of both sides, you must use the [MATH]\pm[/MATH] sign, because there are two square roots.

Proving square root of -1(i) is =1 is the title of the thread. That is not true. Now I admit that cannot read the handwriting is the post.
If the title is incorrect then what is the actual question?

 

[Vara1803]

Proving square root of -1(i) is =1 is the title of the thread. That is not true. Now I admit that cannot read the handwriting is the post.
If the title is incorrect then what is the actual question?

Sorry at first I cannot post it because I did not write a message and because of that I was not able to post, then I thought what happens if I change it from thread to question but it was the same! Then I realised there is an message box then I have written it but forgot to change the question into thread.

 

[pka]

Sorry at first I cannot post it because I did not write a message and because of that I was not able to post, then I thought what happens if I change it from thread to question but it was the same! Then I realised there is an message box then I have written it but forgot to change the question into thread.

Well O.K., but what is your question? It is false the \(1=\) square root of \(-1(i)\).

 

[Vara1803]

Well O.K., but what is your question? It is false the \(1=\) square root of \(-1(i)\).

Please reply what did I do wrong on that equation which gave me the wrong answer

 

[Vara1803]

Please reply what did I do wrong on that equation which gave me the wrong answer

Just saying that it is not correct is not the prof that it is wrong,right?

 

[pka]

Well why will you not tell us what the question actually says.
The complex number \(-1\cdot(\bf i)=-\bf i=\cos\left(\dfrac{-\pi}{2}\right)+{\bf i}\sin\left(\dfrac{-\pi}{2}\right)=\left[\cis\left(\dfrac{-\pi}{2}\right)\right]\)
So one square root of \(-1\cdot(\bf i)\) is \(\left[\cis\left(\dfrac{-\pi}{4}\right)\right]\) the other square root is \(\left[\cis\left(\dfrac{-\pi}{4}+\pi\right)\right]= \left[\cis\left(\dfrac{3\pi}{4}\right)\right]\).
Ar Prof. Peterson told you that each non-zero complex number has two square roots.

 

[Dr.Peterson]

Just saying that it is not correct is not the prof that it is wrong,right?

Yes, it is sufficient proof that it is wrong. We know that i is not equal to 1, because [MATH]i^2 = -1[/MATH] while [MATH]1^2 = 1[/MATH].

Please reply what did I do wrong on that equation which gave me the wrong answer

Here is a slightly improved copy of your work:



As I understand what you wrote, you are not actually trying to solve a problem, but are experimenting with an equation and "discovering" that it shows that i = 1. You want to know what step is wrong.

You are correct at the start that [MATH]i^2 = i^6[/MATH]. But when you take the square root of both sides, you are ignoring the fact that every number has two square roots, and specifically that the square root function is not well-defined for complex numbers, in the sense that it doesn't have all the properties you expect. In particular, the rule you follow to say that i = -i does not apply. Any algebra book when introducing complex numbers should tell you this.

 

[HallsofIvy]

To prove that "a is a square root of b" it is not necessary to calculate the square roots of b, just square a and show that the result is b.

Here it is obvious that -1 is NOT a square root of -i because (-1)^2 is 1, not -i. If you meant that -i is a square root of -1, the proof is that (-i)^2= (-1)^2(i)^2= (1)(-1)= -1.

 

[Vara1803]

Yes, it is sufficient proof that it is wrong. We know that i is not equal to 1, because [MATH]i^2 = -1[/MATH] while [MATH]1^2 = 1[/MATH].



Here is a slightly improved copy of your work:

View attachment 22117

As I understand what you wrote, you are not actually trying to solve a problem, but are experimenting with an equation and "discovering" that it shows that i = 1. You want to know what step is wrong.

You are correct at the start that [MATH]i^2 = i^6[/MATH]. But when you take the square root of both sides, you are ignoring the fact that every number has two square roots, and specifically that the square root function is not well-defined for complex numbers, in the sense that it doesn't have all the properties you expect. In particular, the rule you follow to say that i = -i does not apply. Any algebra book when introducing complex numbers should tell you this.

Thank you for finding my mistake

 

[Vara1803]

Proving square root of -1(i) is =1 is the title of the thread. That is not true. Now I admit that cannot read the handwriting is the post.
If the title is incorrect then what is the actual question?
[/QUOTE/)
See the attachment!!!

 

[Dr.Peterson]

In writing your second line, you appear to be assuming that a^x = a^y implies that x = y, for any value of a. On what grounds do you assume that this is true, even for a = 1? Because 1^2 = 1^3, would you also conclude that 2 = 3?

 

[Vara1803]

In writing your second line, you appear to be assuming that a^x = a^y implies that x = y, for any value of a. On what grounds do you assume that this is true, even for a = 1? Because 1^2 = 1^3, would you also conclude that 2 = 3?

Dont take it too seriously it was just a joke