petarantes
New member
- Joined
- Oct 21, 2016
- Messages
- 15
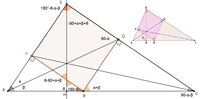
Knowing that BQRP it is a square proves that. =90°
I'm an older student reviewing for a placement test; please check my work.
I tried to relate the theta, alpha and beta angles but all attempts generate equalities
For example 180-theta-alpha -beta - 90 + alpha+beta+theta = 90 --> 90 = 90
I'm an older student reviewing for a placement test; please check my work.
I tried to relate the theta, alpha and beta angles but all attempts generate equalities
For example 180-theta-alpha -beta - 90 + alpha+beta+theta = 90 --> 90 = 90