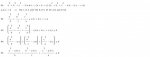You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Prove an inequality a^3/b+b^3/c
- Thread starter Munir
- Start date
- Joined
- Feb 4, 2004
- Messages
- 16,582
Your subject line says "Prove" but your post says "solve". And you say that you "need to solve something like that". But what, exactly, do you need to solve? (or prove?)Hi, I need to solve something like that:
For a,b,c>0 prove:
(a^3)/b + (b^3)/c + (c^3)/a >= ab + bc + ca
I tried to solve this inequality in many ways, but I simply don't khow to do it correctly. Can anyone help me?
Please reply with the full and exact text of the exercise, the complete instructions, and a clear listing of at least one of your efforts at solution, so we can see what's going on. Thank you!
Your subject line says "Prove" but your post says "solve". And you say that you "need to solve something like that". But what, exactly, do you need to solve? (or prove?)
Please reply with the full and exact text of the exercise, the complete instructions, and a clear listing of at least one of your efforts at solution, so we can see what's going on. Thank you!
Hi,
I'm sorry but English is not my mother tongue. I need to prove the inequality for a,b,c >0.
For example I tried to prove it in this way:
a^3/b+b^3/c+c^3/a >=ab+bc+ca //*abc
a^4 c +ab^4 +bc^4 - a^2 b^2 c -ab^2 c^2 +a^2 b c^2 >=0
a^4c -a^2 b^2 c + ab^4 -ab^2 c^2 + bc^4 - a^2 b c^2 >=0
a^2 c (a^2 - b^2) +ab^2 (b^2-c^2) + bc^2 (c^2 - a^2) >=0
a^2 c (a-b)(a+b) +ab^2 (b-c)(b+c) + bc^2 (c-a)(c+a) >=0
I'm stuck in this place, because I don't know how to prove, that for random a,b,c >0: (a-b)>0; (b-c) >0 and (c-a) >0.
I would be grateful for help
D
Deleted member 4993
Guest
Hi,
I'm sorry but English is not my mother tongue. I need to prove the inequality for a,b,c >0.
For example I tried to prove it in this way:
a^3/b+b^3/c+c^3/a >=ab+bc+ca //*abc
a^4 c +ab^4 +bc^4 - a^2 b^2 c -ab^2 c^2 +a^2 b c^2 >=0
a^4c -a^2 b^2 c + ab^4 -ab^2 c^2 + bc^4 - a^2 b c^2 >=0
a^2 c (a^2 - b^2) +ab^2 (b^2-c^2) + bc^2 (c^2 - a^2) >=0
a^2 c (a-b)(a+b) +ab^2 (b-c)(b+c) + bc^2 (c-a)(c+a) >=0
I'm stuck in this place, because I don't know how to prove, that for random a,b,c >0: (a-b)>0; (b-c) >0 and (c-a) >0.
I would be grateful for help
Did you try following relationship:
a3 + b3 + c3 - 3abc = (a + b + c)(a2 + b2 + c2 - ab - bc - ca)
Did you try following relationship:
a3 + b3 + c3 - 3abc = (a + b + c)(a2 + b2 + c2 - ab - bc - ca)
I don't see how this relationship should help me, so no, I didn't try it.
- Joined
- Feb 4, 2004
- Messages
- 16,582
Did you try using the relationship that was provided to you in the prior reply?I still don't have any idea how to prove this inequality. Can anyone help me?
With you Munir ....
I don't see it either Munir, why not ask for an additional clue, get us off of the rocks. My best was to ship the right side to the left side and regroup and then to try and simplify and factor:
Typical,
\(\displaystyle \frac{{{a^3}}}{b} - ab = \frac{{{a^3} - {a^{}}{b^2}}}{b} = \frac{{a({a^2} - {a^{}}{b^2})}}{b} = \frac{{a(a - b)(a + {b^{}})}}{b}\)
overall,
\(\displaystyle \frac{{a(a - b)(a + {b^{}})}}{b} + \frac{{b(b - c)(b + {c^{}})}}{c} + \frac{{c(c - a)(c + {a^{}})}}{a} \ge 0\)
Alas, no common factors.
Overall you would think there might be some way of proving this based on the symmetry, i.e. each side has three terms each of which, respectively, is a function of the same two variables, sort of spherical perhaps, i.e starting from (0, 0, 0) increasing any single variable a single unit results in the same displacement if you ignore direction. Just musing.
I don't see how this relationship should help me, so no, I didn't try it.
I don't see it either Munir, why not ask for an additional clue, get us off of the rocks. My best was to ship the right side to the left side and regroup and then to try and simplify and factor:
Typical,
\(\displaystyle \frac{{{a^3}}}{b} - ab = \frac{{{a^3} - {a^{}}{b^2}}}{b} = \frac{{a({a^2} - {a^{}}{b^2})}}{b} = \frac{{a(a - b)(a + {b^{}})}}{b}\)
overall,
\(\displaystyle \frac{{a(a - b)(a + {b^{}})}}{b} + \frac{{b(b - c)(b + {c^{}})}}{c} + \frac{{c(c - a)(c + {a^{}})}}{a} \ge 0\)
Alas, no common factors.
Overall you would think there might be some way of proving this based on the symmetry, i.e. each side has three terms each of which, respectively, is a function of the same two variables, sort of spherical perhaps, i.e starting from (0, 0, 0) increasing any single variable a single unit results in the same displacement if you ignore direction. Just musing.
Last edited by a moderator:
D
Deleted member 4993
Guest
The reason I had suggested the "relation" is as follows:I don't see it either Munir, why not ask for an additional clue, get us off of the rocks. My best was to ship the right side to the left side and regroup and then to try and simplify and factor:
Typical,
\(\displaystyle \frac{{{a^3}}}{b} - ab = \frac{{{a^3} - {a^{}}{b^2}}}{b} = \frac{{a({a^2} - {a^{}}{b^2})}}{b} = \frac{{a(a - b)(a + {b^{}})}}{b}\)
overall,
\(\displaystyle \frac{{a(a - b)(a + {b^{}})}}{b} + \frac{{b(b - c)(b + {c^{}})}}{c} + \frac{{c(c - a)(c + {a^{}})}}{a} \ge 0\)
Alas, no common factors.
Overall you would think there might be some way of proving this based on the symmetry, i.e. each side has three terms each of which, respectively, is a function of the same two variables, sort of spherical perhaps, i.e starting from (0, 0, 0) increasing any single variable a single unit results in the same displacement if you ignore direction. Just musing.
a^3/b - ca + b^3/c - ab + c^3/a - bc ≥ 0
=(a^3 - abc)/b + (b^3 -abc)/c + (c^3 - abc)/a
If a≤b≤c
(a^3 - abc)/b + (b^3 -abc)/c + (c^3 - abc)/a ≥ (a^3 - abc)/c + (b^3 -abc)/c + (c^3 - abc)/c
(a^3 - abc)/c + (b^3 -abc)/c + (c^3 - abc)/c = (a^3 + b^3 + c^3 - 3abc)/c
and so forth.......
Last edited by a moderator:
forth, on, and so ... please
If possible when you have time ... (I don't know how to make these images larger; I snap the entire screen in shooting them. If anybody knows I will gladly repost... ?)



Salamat po.
The reason I had suggested the "relation" is as follows:
a^3/b - ca + b^3/c - ab + c^3/a - bc ≥ 0
=(a^3 - abc)/b + (b^3 -abc)/c + (c^3 - abc)/a
If a≤b≤c
(a^3 - abc)/b + (b^3 -abc)/c + (c^3 - abc)/a ≥ (a^3 - abc)/c + (b^3 -abc)/c + (c^3 - abc)/c
(a^3 - abc)/c + (b^3 -abc)/c + (c^3 - abc)/c = (a^3 + b^3 + c^3 - 3abc)/c
and so forth.......
If possible when you have time ... (I don't know how to make these images larger; I snap the entire screen in shooting them. If anybody knows I will gladly repost... ?)
Salamat po.
Attachments
Last edited: