If in a triangle ABC, angle A is 30°, angle B is 50° prove that c^2=b*(a+b).
Sides a, b, and c are opposite of angles A, B, and C respectively.
I think the problem should not be very hard as it was in the intermediate section of my math textbook. But I really can't see how to prove it.
I have been trying to solve this problem for a few hours. I've tried to draw altitudes from the angles and use the Pythagorian theorem on the right triangles that were formed. I've also tried drawing squares on the sides of the triangle and tried to equate the areas of the rectangles but I am not really sure whether it is right to do so.
I thought of finding identical triangles formed by the altitudes and prove some ratio but I don't know how to do it. I've actually asked my math teacher too but she couldn't prove the equation.
Here's the picture of the problem for convenience.
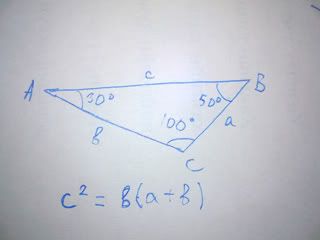
Sides a, b, and c are opposite of angles A, B, and C respectively.
I think the problem should not be very hard as it was in the intermediate section of my math textbook. But I really can't see how to prove it.
I have been trying to solve this problem for a few hours. I've tried to draw altitudes from the angles and use the Pythagorian theorem on the right triangles that were formed. I've also tried drawing squares on the sides of the triangle and tried to equate the areas of the rectangles but I am not really sure whether it is right to do so.
I thought of finding identical triangles formed by the altitudes and prove some ratio but I don't know how to do it. I've actually asked my math teacher too but she couldn't prove the equation.
Here's the picture of the problem for convenience.


