Proportions Problem

[Iceycold12]

Hello

The time that it takes to fill a fish tank depends upon the rate at which the water is flowing. It
takes 40 minutes to fill the fish tank at the rate of 3 gallons per minute. How many minutes
will it take to fill the fish tank at the rate of 4 gallons per minute?

Step I. Set up proportion

Step II. Solve proportion

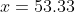
Which is Answer D, but I got the Answer Key to check my answer and the answer is actually B, 30. I can see it 10 less minutes if the rate increases a gallon per minute but I think here proportions > logic?

Thanks.

 

[soroban]

Hello, Iceycold12!

Do we have to use proportions?

The time that it takes to fill a fish tank depends upon the rate at which the water is flowing.
It takes 40 minutes to fill the fish tank at the rate of 3 gallons per minute.
How many minutes will it take to fill the fish tank at the rate of 4 gallons per minute?

At 3 gal/min, it takes 40 minutes to fill the tank.
Hence, the tank's capacity is: /\(\displaystyle 3\cdot40 \:=\:120\text{ gallons}\)

At 4 gal/min, it will take: .\(\displaystyle \dfrac{120\text{ gal}}{4\text{ gal/min}} \:=\:30\text{ minutes}\)

 

[Iceycold12]

I see, that's one tricky problem then. Thanks a lot! I sort of see why we can't use proportions here, since the tank actually has a limit to the amount of water in the fish tank.

 

[HallsofIvy]

I see, that's one tricky problem then. Thanks a lot! I sort of see why we can't use proportions here, since the tank actually has a limit to the amount of water in the fish tank.

No, the "limit'" has nothing to do with it. The problem is that this is simply not a "direct" proportion. The faster the water goes in (the higher the speed is) the less time it takes to fill the tank. This is an inverse proportion problem.
But the real point is to think about what is happening- to find the time it takes to fill a tank at a given rate, you need to know the volume of the tank.