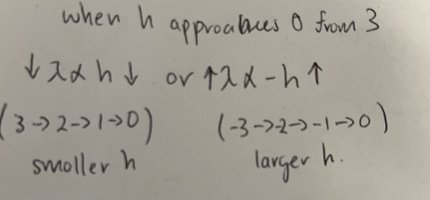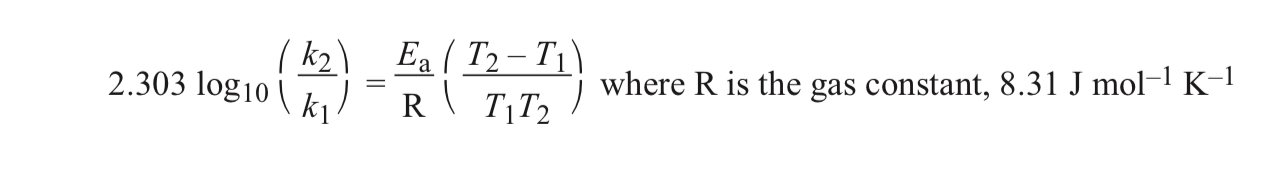Hi there,
Not sure where to post this as this is a weird question, hope I'm in the right space. I'm prepping for a standardised test where isolating variables/getting rid of constants to find relationships between variables is a key skill. I've read the rules but I don't have specific questions as I am trying to practise the general skill itself. It looks something like this:

Question: If there is a negative sign in front of a variable, do I keep the negative sign in the proportionality relationship or get rid of it? I've been told conflicting things, and was under the assumption that I should be removing the negative sign.

Not sure where to post this as this is a weird question, hope I'm in the right space. I'm prepping for a standardised test where isolating variables/getting rid of constants to find relationships between variables is a key skill. I've read the rules but I don't have specific questions as I am trying to practise the general skill itself. It looks something like this:

Question: If there is a negative sign in front of a variable, do I keep the negative sign in the proportionality relationship or get rid of it? I've been told conflicting things, and was under the assumption that I should be removing the negative sign.

Attachments
Last edited: