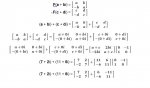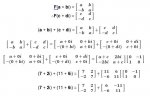Proof for complex numbers addition and multiplication in 2x2 matrices

[MathematicallyChallenged]

Firstly, want to apologize for having to ask this. I have no formal maths training and am trying to help my kid out here. We were able to define some things but not able to show the working of it nor any examples.

The problem is as follows:

Prove that addition of complex numbers is equivalent to the addition of the corresponding 2x2 matrices and that multiplication of complex numbers is equivalent to the multiplication of the corresponding 2x2 matrices.

Verify the reasonableness of these results using numerical examples.

We were able to piece this together so far:

• We can realize complex numbers as certain 2 x 2 matrices with real entries.
• A complex number is an expression of the form a + bi where a and b are real numbers.
• Let C denote the set of all complex numbers.
• Any real number a is a complex number since a can be written as a + 0i
• The complex numbers of the form bi = 0 + bi
• Let i and − i denote the imaginary numbers 1i and − 1i respectively.
• Addition is defined by (a + bi ) + (c + di ) = (a + c) + (b + d)i
• Multiplication is defined by (a + bi )(c + di ) = (ac − bd) + (ad + bc)i

• We assign to each complex number a + bi the 2× 2 matrix
• We define a function F whose domain is C and whose codomain is the set of all 2× 2 matrices with real entries

THE RULE


AND SOME OF THIS CRAP WE TRIED






HELP!!! I truly suck at this and my I don't want my daughter to fail because of my shortcomings as a father!

 

[stapel]

Prove that addition of complex numbers is equivalent to the addition of the corresponding 2x2 matrices and that multiplication of complex numbers is equivalent to the multiplication of the corresponding 2x2 matrices.

Verify the reasonableness of these results using numerical examples.

It looks as though what you have attempted is the declaration that the various processes are the same, rather than a demonstration that the processes are equivalent. There is a difference!

Let's use your two generic complex numbers, \(\displaystyle \, a\, +\, bi\, \) and \(\displaystyle \, c\, +\, di.\, \) Then their sum is:

. . . . .\(\displaystyle (a\, +\, bi)\, +\, (c\, +\, di)\, =\, a\, +\, bi\, +\, c\, +\, di\, =\, (a\, +\, c)\, +\, (b\, +\, d)i\)

...and their product is:

. . . . .\(\displaystyle (a\, +\, bi)\, \cdot\, (c\, +\, di)\, =\, ac\, +\, bci\, +\, adi\, +\, bdi^2\, =\, (ac\, -\, bd)\, +\, (bc + ad)i\)

Now we need to define an equivalence. We don't say that complex numbers in rectangular form are (or "equal") matrices, but we define an equivalence whereby we can take the one and restate it as the other:

. . . . .\(\displaystyle \mbox{Let }\, a\, +\, bi\, \mbox{ be restated as }\, \left[\begin{array}{cc}a&b\\-b&a\end{array}\right]\)

Then show that adding the two matrices for the two generic complex numbers gives one matrix which can be restated as the sum of the two complex numbers.

. . . . .\(\displaystyle \left[\begin{array}{cc}a&b\\-b&a\end{array}\right]\, +\, \left[\begin{array}{cc}c&d\\-d&c\end{array}\right]\, =\, \left[\begin{array}{cc}a+c&b+d\\-b-d&a+c\end{array}\right]\, =\, \left[\begin{array}{cc}a+c&b+d\\-(b+d)&a+c\end{array}\right]\)

This last matrix would be equivalent to the complex number \(\displaystyle \, (a\, +\, c)\, +\, (b\, +\, d)i.\,\) So this works. What about multiplying?

. . . . .\(\displaystyle \left[\begin{array}{cc}a&b\\-b&a\end{array}\right]\left[\begin{array}{cc}c&d\\-d&c\end{array}\right]\, =\, \left[\begin{array}{cc}ac-bd&ad+bc\\-bc-ad&-bd+ac\end{array}\right]\, =\, \left[\begin{array}{cc}ac-bd&ad+bc\\-(ad+bc)&ac-bd\end{array}\right]\)

To what complex number would this be equivalent?