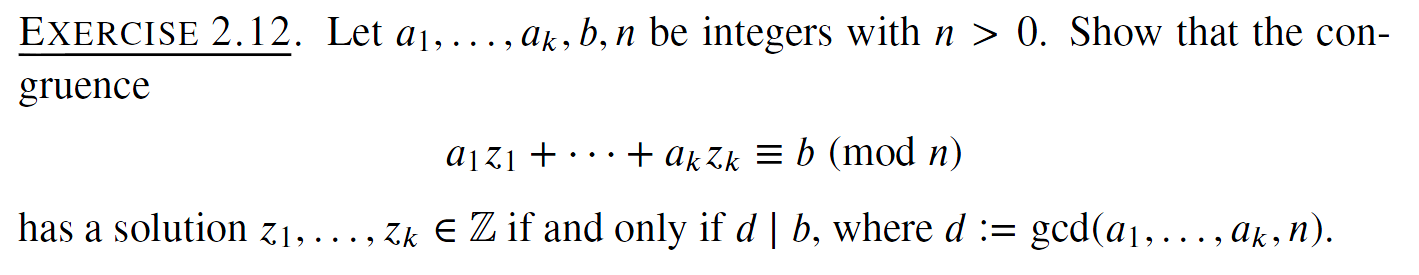You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Proof a Linear Congruence
- Thread starter KimO
- Start date
- Joined
- Feb 4, 2004
- Messages
- 16,550
Let [FONT=MathJax_Math-italic]a[FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Main]…[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Math-italic]a[/FONT][FONT=MathJax_Math-italic]k[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Math-italic]b[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Math-italic]n[/FONT]a1,…,ak,b,n[/FONT] be integers with [FONT=MathJax_Math-italic]n[FONT=MathJax_Main]>[/FONT][FONT=MathJax_Main]0[/FONT]n>0[/FONT].
Show that the congruence [FONT=MathJax_Math-italic]a[FONT=MathJax_Main]1[/FONT][FONT=MathJax_Math-italic]z[/FONT][FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main]+[/FONT][FONT=MathJax_Main]⋯[/FONT][FONT=MathJax_Main]+[/FONT][FONT=MathJax_Math-italic]a[/FONT][FONT=MathJax_Math-italic]k[/FONT][FONT=MathJax_Math-italic]z[/FONT][FONT=MathJax_Math-italic]k[/FONT][FONT=MathJax_Main]≡[/FONT][FONT=MathJax_Math-italic]b[/FONT][FONT=MathJax_Main]([/FONT][FONT=MathJax_Main]mod n[/FONT][FONT=MathJax_Main])[/FONT]a1z1+⋯+akzk≡b(mod n)[/FONT] has a solution [FONT=MathJax_Math-italic]z[FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Main]…[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Math-italic]z[/FONT][FONT=MathJax_Math-italic]k[/FONT][FONT=MathJax_Main]∈[/FONT][FONT=MathJax_AMS]Z[/FONT]z1,…,zk∈Z[/FONT] if and only if [FONT=MathJax_Math-italic]d[FONT=MathJax_Main]|[/FONT][FONT=MathJax_Math-italic]b[/FONT]d|b[/FONT], where
[FONT=MathJax_Math-italic]d[FONT=MathJax_Main]:=[/FONT][FONT=MathJax_Main]gcd[/FONT][FONT=MathJax_Main]([/FONT][FONT=MathJax_Math-italic]a[/FONT][FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Main]…[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Math-italic]a[/FONT][FONT=MathJax_Math-italic]k[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Math-italic]n[/FONT][FONT=MathJax_Main])[/FONT]d:=gcd(a1,…,ak,n)[/FONT].
I tried to find solution this way but i didn't bring the end
There exist [FONT=MathJax_Math-italic]z[FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Main]…[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Math-italic]z[/FONT][FONT=MathJax_Math-italic]k[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Math-italic]z[/FONT][/FONT]such that [FONT=MathJax_Math-italic]a[FONT=MathJax_Main]1[/FONT][/FONT][FONT=MathJax_Math-italic]z[FONT=MathJax_Main]1[/FONT][/FONT][FONT=MathJax_Main]+[/FONT][FONT=MathJax_Main]⋯[/FONT][FONT=MathJax_Math-italic]a[FONT=MathJax_Math-italic]k[/FONT][/FONT][FONT=MathJax_Math-italic]z[FONT=MathJax_Math-italic]k[/FONT][/FONT][FONT=MathJax_Main]+[/FONT][FONT=MathJax_Math-italic]n[/FONT][FONT=MathJax_Math-italic]z[/FONT][FONT=MathJax_Main]=[/FONT][FONT=MathJax_Main]gcd[/FONT][FONT=MathJax_Main]([/FONT][FONT=MathJax_Math-italic]a[FONT=MathJax_Main]1[/FONT][/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Main]…[/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Math-italic]a[FONT=MathJax_Math-italic]k[/FONT][/FONT][FONT=MathJax_Main],[/FONT][FONT=MathJax_Math-italic]n[/FONT][FONT=MathJax_Main])[/FONT][FONT=MathJax_Main].[/FONT]
The cramped formatting and textual "stutters" make this post very difficult to read. The following is my guess as to the intended meaning:
Let a1, a2, ..., ak, b, and n be integers, with n > 0.
Suppose you have the following congruence:
. . . . .a1z1 + a2z2 + ... + akzk = b(mod n)
Show that this congruence has a solution z1, z2, ..., zk, where the zi are integers, if and only if d divides b, where d is the GCD of a1, a2, ..., ak, and n.
Is this correct?
Thank you!
If the gcd divides b, then as the equation \(\displaystyle kn+\sum a_ix_i = d\) has some solution \(\displaystyle (k,x_1,...,x_n)\), letting \(\displaystyle z_i=\frac{b}{d}x_i, k'=\frac{b}{d}k\) gives what you want.
Conversely, if \(\displaystyle k'n+\sum a_iz_i = b\), then you may* use the fact that the gcd is the smallest linear combination, and divides all others, to get the result.
*You may need to prove this.
Conversely, if \(\displaystyle k'n+\sum a_iz_i = b\), then you may* use the fact that the gcd is the smallest linear combination, and divides all others, to get the result.
*You may need to prove this.