I need help with these problems: (12), (20), and (26) are not exercises; they're just statements of functions.
In order to be an exercise, there needs to be given instruction(s).
What have you been asked to do in exercises (12), (20), and (26).
12. R(t)= (t+e^t)(3-sq root(t)) Are you asked to find R '(t) ?
Since R is a product of two other functions in t, we can use the Product Rule to find the first derivative of R.
If this is what you've been asked to do, then have you looked up the Product Rule? Have you used it at all, before? Do you have a textbook with any examples.
WHY ARE YOU STUCK?
If you can make any effort at all, then please show your work, thus far.
BtW: we can type square roots like this: (3 - sqrt[t])
20. z=w^3/2(w+ce^w) This typing is ambiguous because grouping symbols are missing. Which of the following are you trying to type?
\(\displaystyle z \;=\; \frac{w^3}{2} \cdot (w \;+\; c \cdot e^w)\)
\(\displaystyle z \;=\; w^{3/2} \cdot (w \;+\; c \cdot e^w)\)
What have you been asked to do? Find the derivative of z with respect to c ? With respect to w?
Why are you making us guess?
26. f(x)= ax+b/cx+d Again, your typing is ambiguous. Is this supposed to be a ratio of two polynomials? Are you supposed to find f '(x) ?
\(\displaystyle f(x) \;=\; ax \;+\; \frac{b}{cx} \;+\; d\)
\(\displaystyle f(x) \;=\; ax \;+\; \frac{b}{c} \cdot x \;+\; d\)
\(\displaystyle f(x) \;=\; \frac{ax \;+\; b}{cx \;+\; d}\)
If you've been asked to find f '(x), and f is a ratio of two polynomials, then use the Quotient Rule. Have you used this rule before? If you don't understand it, then please ask specific questions.
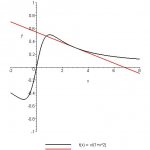
36. (a) The curve y=x/(1+x^2) is called a serpentine. Find an equation of the tangent line to this curve at the point (3, 0.3).
(b) Illustrate part (a) by graphing the curve and the tangent line on the same screen.
Here, you've properly typed grouping symbols around the denominator!
Find the first derivative of y by using either the Product Rule or the Quotient Rule, according to your preference. Evaluate y-prime at x = 3 to get the slope of the line. Then use the Point-Slope formula to write the equation of the tangent line.
You've made no statements about why you're stuck on (36) either. Are we playing a guessing game?
The way it works at this web site is: (1) You explain to us what you need to know; (2) we guide you through your specific questions.
So, show us what you already know about these exercises, followed by specific questions about what you don't understand.