I have a russian math teacher that does not teach he has had tenor for the last 3 years and can not be fired he just stops getting bonuses here at ohio state universaty... And no im not just whining. the class average is a 42... I need help on his impossible to us take home test.
Any problems would help if anybody can help me with them.
Thanks in advance to anyone.
2) Use newton's method with initial aproximation (a) x0=sqrt(3) (b)x0=1.7320508 (c)x0=1.73205081 to solve the equation x^5-81x=0. Find the exact limits.
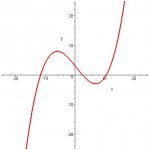
3) Find a cubic function g(x)=ax^3+bx^2+cx+d that has a local maximum value of 8 at -6 and a local minimum value of -3 at 7.
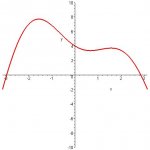
4) Sketch the graph of f(x)=(4x^3+9x^2-3)e^(3x). Not using a graphing utility.
5) Sketch the graph of g(x)=(10x^3+5x^2+6x-5)/(x^2+8x-4). Not using a graphing utility
7) Find correct to six decimal places the coordinates of the points on the curve y=cosx that are closest to the point (0,-1).
8) Find the maxima and minima of the function f(x)=(3x-2)sinx+3cosx+1 on the interval [-pi,pi].
9) LEt g(x)=3x^4+x^2-9. a) Find the intervals on which g is increasing or decreasing. (b) find the intervals of concavity and the inflection points.
10) Find the inflection points of the curve y=(x^3-9x^2-30x-41)e^x correct to six decimal places.
11) If g(-1)=3, g(1)=5 and g''(x) greater than or equal to 6, how large can g(0) possibly be>
Any problems would help if anybody can help me with them.
Thanks in advance to anyone.
2) Use newton's method with initial aproximation (a) x0=sqrt(3) (b)x0=1.7320508 (c)x0=1.73205081 to solve the equation x^5-81x=0. Find the exact limits.
3) Find a cubic function g(x)=ax^3+bx^2+cx+d that has a local maximum value of 8 at -6 and a local minimum value of -3 at 7.
4) Sketch the graph of f(x)=(4x^3+9x^2-3)e^(3x). Not using a graphing utility.
5) Sketch the graph of g(x)=(10x^3+5x^2+6x-5)/(x^2+8x-4). Not using a graphing utility
7) Find correct to six decimal places the coordinates of the points on the curve y=cosx that are closest to the point (0,-1).
8) Find the maxima and minima of the function f(x)=(3x-2)sinx+3cosx+1 on the interval [-pi,pi].
9) LEt g(x)=3x^4+x^2-9. a) Find the intervals on which g is increasing or decreasing. (b) find the intervals of concavity and the inflection points.
10) Find the inflection points of the curve y=(x^3-9x^2-30x-41)e^x correct to six decimal places.
11) If g(-1)=3, g(1)=5 and g''(x) greater than or equal to 6, how large can g(0) possibly be>