Problem finding delta....

[johnny4lsu]

Problem:

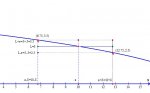
let f(x)=sqrt(19-x) and lim x-->10 f(x)=3 . Use the graph (or table) to find a value delta whenever epsilon=.5

Can someone please help me with this problem? Thanks

 

[johnny4lsu]

can anyone get me started please?

 

[galactus]

Here is a graph, John, of what is going on. The idea is to find \(\displaystyle |f(x)-L|<{\epsilon}\), whenever \(\displaystyle 0<|x-a|<{\delta}\)

In this case, find \(\displaystyle |\sqrt{19-x}-3|<0.5\), whenever \(\displaystyle 0<|x-10|<{\delta}\)

We should expect that \(\displaystyle \sqrt{19-x}-3<0.5\) whenever \(\displaystyle |x-10|\) is small enough.

We want to know how small |x-10| should be to make sure that \(\displaystyle |\sqrt{19-x}-3|<0.5\)

The graph says a lot. See where delta and epsilon are?. I tried labeling them well enough so that you have a good picture of the concept.

 

[johnny4lsu]

ok, so delta has two values here? so delta would be 2.75 right?

 

[galactus]

No, that's the values of x. Look closer

 

[johnny4lsu]

so 2.75 is delta
i see that delta is also 3.25. would i use the smaller value 2.75?

 

[BigGlenntheHeavy]

On the left side of x=10, we need |x-10|<|6.75-10|=3.25.

On the right side, we need |x-10|<|12.75-10| = 2.75.

For both of these conditions to be satisfied at once, we need the more restrictive of the two to hold, that is

|x-10|<2.75. So we can choose ? = 2.75 or any smaller positive number.

 

[BigGlenntheHeavy]

Another way:

\(\displaystyle We \ have \ | \sqrt(19-x)-3|<\frac{1}{2} \ whenever \ 0<|x-10|<\delta, \ find \ \delta.\)

\(\displaystyle |[ \sqrt(19-x)-3]\frac{[\sqrt(19-x)+3]}{[\sqrt(19-x)+3]}|<\frac{1}{2}.\)

\(\displaystyle |\frac{19-x-9}{\sqrt(19-x)+3}|<\frac{1}{2}, \\) \(\displaystyle \frac{|10-x|}{|\sqrt(19-x)+3|}<\frac{1}{2}.\)

\(\displaystyle |10-x| \ = \ |x-10|, \ Why?\) \(\displaystyle Ergo \ |x-10|<\frac{|\sqrt(19-x)+3|}{2}=\delta.\)

Since by the above graph, 6.75<x<12.75, we will plug these into our above inequality.

\(\displaystyle Hence, \ |x-10|<2.75=\delta_1 \ and \ |x-10|<3.25=\delta_2\)

\(\displaystyle Taking \ \delta_1 \ to \ satisfy \ both \ inequalities, \ we \ have \ \delta \ = \ 2.75 \ or \ any \ smaller \ positive \ number.QED\)