Problem calculating initial number in percentage increase problem

K

Kai_AndersonBradley

New member
Joined
Dec 17, 2020
Messages
7
Hi there, I'm studying for a maths exam coming up and i've come across this problem which is very likely to be in the test. I can calculate percentage increase/decrease fine, but this question stumps me. As you can see, I've got to find the "Male annual income", and i've initially worked out the solution incorrectly. Can someone please help and explain this problem to me? How do I go about solving?
 

Attachments

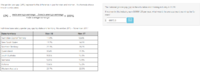
  • Screenshot 2020-12-18 122220.png
    Screenshot 2020-12-18 122220.png
    41.9 KB · Views: 10
You seem to have added 11.3 (which is a percentage) onto 69061.2 (which is a dollar amount) to get 69072.5. You can't add two things which are not in the same units.
Try this. Let x be the male average earnings. Use the formula they give you to get an equation involving x, 11.3, and 69061.20. Then solve for x.
 
Last edited:
Kai_AndersonBradley said:
… please help and explain this problem…
Click to expand...
Hi Kai. They state the formula gives the difference in pay between men and women, but that description is not quite correct. The difference is actually what appears in the formula's numerator. The formula then divides that difference by the men's earnings. Dividing the difference by what the men earn causes the pay gap to be stated as a percent of the men's earnings.

So, when they say GPG is 11.3%, they're saying the difference in pay is 11.3% of what men get.

For example, if men earn 10,000 and women earn 3,333.33 then the difference is 6,666.67 and we would say that difference is two-thirds of what men make -- that is, the gender pay gap is 66.66% of what men make.

GPG% = (10000 - 3333.33)/10000 × 100%

GPG% = 0.666667 × 100%

GPG% = 66.6667%

For the next example, I define the following symbols.

M = average male earnings
F = average female earnings

Now we may write the formula as:

GPG% = (M - F)/M × 100%

When GPG is 50% and women earn 10,000 then what do men earn?

Substitute the known values for GPG and F, in the formula:

50% = (M - 10000)/M × 100%

Personally, I prefer to not write percent signs in equations; I would use the decimal form of 50%, instead. That is, I'll remove the percent sign from each side, and then divide each side by 100:

0.50 = (M - 10000)/M

0.50M = M - 10000

10000 = 0.50M

M = 20000

When GPG is 50% and women earn 10,000, then men earn 20,000.

If you need more help with this, then please post your questions and/or what you've tried.

?
 
Thank you for your replies.

I understand what you say when you explained that if the GPG is 50% or 0.5 then the male annual income is basically double that of the female. I found it a little more tricky to confidently work out the 11.3% GPG.

So, in this instance, I have converted the 11.3% into a decimal (0.113) and multiplied this by the average Female annual income, then added the result to the given dollar amount ($69 061.20) and got back $76 865.12. Do you believe that this would be the correct answer?

Apologies, It's a little tricky to get this validated by the practice exam as I can't cherry pick questions I got wrong, I need to re-sit the entire exam and it becomes a bit frustrating just for one question.

Cheers!
 
Kai_AndersonBradley said:
… I have converted the 11.3% into a decimal (0.113) and multiplied this by the average Female annual income, then added the result to the given dollar amount ($69 061.20) and got back $76 865.12…
Click to expand...
Hi. Your steps don't use the given formula, so your result doesn't work in the formula:

(76865.12 - 69061.20)/76865.12 = 0.102

In my worked example above (post #3), I'd started by substituting the known values into the formula. That gave an equation to solve for M. Do you know how to solve the equation:

(M - 69061.25)/M = 0.113

?
 
No I don't know how to solve for M, sorry. Can you explain it to me? (Hoping you haven't already and I'm not just a peanut)
 
\(\displaystyle \frac{M-69061.20}{M} = 0.113\)

Multiply both sides by \(\displaystyle M\) and you get

\(\displaystyle M-69061.20=0.113M\)

Now subtract \(\displaystyle 0.113M\) from both sides and you get

\(\displaystyle 0.887M-69061.20=0\)

Can you finish it?

(BTW this is what I suggested you do in Post #2)
 
Harry_the_cat said:
\(\displaystyle \frac{M-69061.20}{M} = 0.113\)

Multiply both sides by \(\displaystyle M\) and you get

\(\displaystyle M-69061.20=0.113M\)

Now subtract \(\displaystyle 0.113M\) from both sides and you get

\(\displaystyle 0.887M-69061.20=0\)

Can you finish it?

(BTW this is what I suggested you do in Post #2)
Click to expand...

Sadly no, I can't finish it. I wasn't aware this was an algebraic problem haha. It seems I would need to start at the beginning of algebra to be able to tackle a problem like this.
 
Otis said:
What kind of practice exam are you trying to finish, Kai? (We use algebra to solve such equations.) Are you preparing to start a math class or have you already started one?

?
Click to expand...

It is a Police entrance exam. There are a bunch of problems with varying degrees of difficulty, this being one of the harder ones. I was really hoping I could study and be able to do well with questions like these, however my exam is in just over a month and I'm not sure I'd be able to tackle these types of questions. As well as study for the other aspects of the entrance exams, I am also working full time and a father, so my time is very limited.

Thank you for your attempt at helping me, I really appreciate it
 
Kai_AndersonBradley said:
It is a Police entrance exam …
Click to expand...
I wish I'd known. Yes, fundamental algebra is how we calculate an unknown value in a formula, when we're given all the other values. Studying beginning algebra shows us also a new way of thinking: symbolic reasoning. That is, algebra shows us how to understand and solve problems using symbols to represent numbers and equations to represent relationships between them (formulas).

If you're not able to take the exam later, I'd suggest skipping the difficult math exercises because your plate is already full so one month wouldn't give you a chance to absorb the concepts.

\(\;\)
 
Kai_AndersonBradley said:
It is a Police entrance exam. There are a bunch of problems with varying degrees of difficulty, this being one of the harder ones. I was really hoping I could study and be able to do well with questions like these, however my exam is in just over a month and I'm not sure I'd be able to tackle these types of questions. As well as study for the other aspects of the entrance exams, I am also working full time and a father, so my time is very limited.

Thank you for your attempt at helping me, I really appreciate it
Click to expand...
All the best with the entrance exam.
 
Thought you guys might like to know, I did a bit of learning and managed to figure this out :)

The answer for the male average is $77 859.30.

I changed the 0.887M to 0.887/M and did this for both sides of the equation, leaving M=77859.30.

I then checked my answer by plugging this result into the formula given and it worked out to be 11.3.

Thank you both for your explanations and time. I appreciate it!
 
Kai_AndersonBradley said:
… I changed the 0.887M to 0.887/M and did this for both sides of the equation…
Click to expand...
Hi Kai. I'm not sure how you made that change, but you got the answer. Good for you. For comparison to what you studied, here are some last steps.

0.887M - 69061.20 = 0

Add 69061.20 to each side

0.887M - 69061.20 + 69061.20 = 0 + 69061.20

Simplify each side

0.887M = 69061.20

Divide each side by 0.887

0.887M / 0.887 = 69061.20 / 0.887

Simplify each side

M = 77859.30

?
 
Otis said:
Hi Kai. I'm not sure how you made that change..
Click to expand...

Sorry, I shouldn't have said "change". What I meant is what you had just explained. I added 69061.20 to both sides, then I divided both sides by 0.887 and simplified each side, each time.

:) I'm pretty happy with myself haha, thanks for all your help, Mate
 
You must log in or register to reply here.
Top