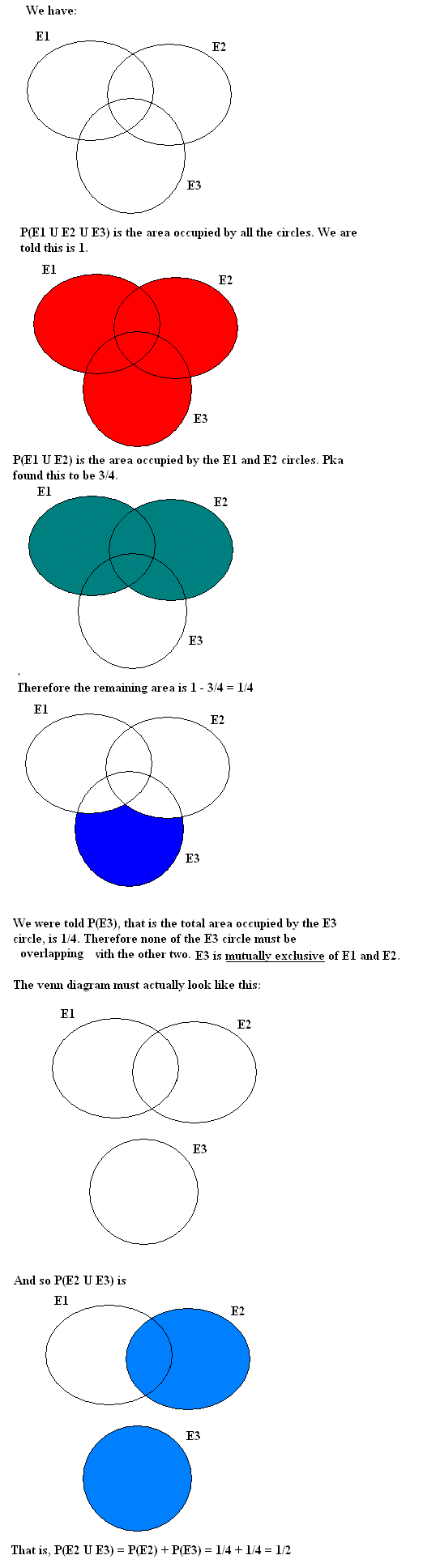Probability - Independant Events

[mattgad]

Hello.

This question is really puzzling me.

The 3 events E1, E2 and E3 are defined in the same sample space and . $\displaystyle P(E1 u E2 u E3) = 1$. The events E1 and E2 are independant. Given $\displaystyle P(E1) = 2/3$. $\displaystyle P(E2) = 1/4$ and $\displaystyle P(E3) = 1/4$

Find:
a) $\displaystyle P(E1 u E2)$
b) $\displaystyle P(E2 u E3)$

I've looked through my book for the rules on independant events but cannot seem to find it. The answers are in the back of the book, a) 3/4 b) 1/2. How do I go about doing these?

Thanks

 

[pka]

\(\displaystyle \
\begin{array}{l}
P(E_1 \cup E_2 ) = P(E_1 ) + P(E_2 ) - P(E_1 \cap E_2 ) = P(E_1 ) + P(E_2 ) - P(E_1 )P(E_2 ) \\
P(E_1 \cup E_2 ) = (2/3) + (1/4) - (1/6) \\
\end{array}\)

 

[Unco]

G'day, Matt.

In case you're wondering, if E1 and E2 are independent then P(E1 /\ E2) = P(E1) * P(E2).

For the second one:

 

[mattgad]

Thankyou guys for all your hard work, I now fully understand how to get to the answer.

Cheers