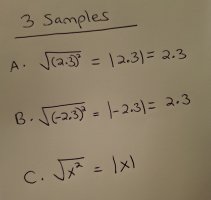Principal of Square Root

[mathdad]

Michael Sullivan goes on to say this:

". . .Since the principal square root is non-negative, we need an absolute value to ensure the nonnegative result."

Let a^2 = any real number => 0.

Then sqrt{a^2} = | a |, according to the textbook. Way back in my elementary school and middle school days, math teachers NEVER taught the square root principal.

To me, the square root of any positive number or 0 is always a positive answer, especially when searching for distance.

For example, sqrt{25} = 5 and -5 back in my early childhood days. In college algebra, the sqrt{25} = | 5 | to assure a positive result.
See attachment.

When does taking the square root yield a positive and negative result?

 

[Dr.Peterson]

When does taking the square root yield a positive and negative result?

A (positive) number has two square roots, one positive and one negative. When you take "the" square root, you take only the positive one, which we call the principal root. But for some purposes you want all roots, which is different.

The point of what you are reading is that since the (principal) square root of a number is (by definition) non-negative, we can't say in general that [imath]\sqrt{x^2}=x[/imath]; that would not be true when [imath]x<0[/imath]. The absolute value is used, [imath]\sqrt{x^2}=|x|[/imath], to make a statement that will always be true.

On the other hand, when you are solving a problem for which both positive and negative answers make sense, we can express both roots as [imath]\pm\sqrt{x}[/imath]. Thus, for example, the solution of [imath]x^2=4[/imath] consists of both roots, [imath]x=\pm\sqrt{4}=\pm2=2,-2[/imath]. Here we have to explicitly indicate that both signs are to be taken.

By the way, it is not "the principal of the square root", or "the square root principal"; "principal" means the primary, or main, root, the one we use by default. The principal square root of 4 is [imath]\sqrt{4}=2[/imath]; the other one has to be explicitly indicated as [imath]-\sqrt{4}=-2[/imath].

 

[mathdad]

A (positive) number has two square roots, one positive and one negative. When you take "the" square root, you take only the positive one, which we call the principal root. But for some purposes you want all roots, which is different.

The point of what you are reading is that since the (principal) square root of a number is (by definition) non-negative, we can't say in general that [imath]\sqrt{x^2}=x[/imath]; that would not be true when [imath]x<0[/imath]. The absolute value is used, [imath]\sqrt{x^2}=|x|[/imath], to make a statement that will always be true.

On the other hand, when you are solving a problem for which both positive and negative answers make sense, we can express both roots as [imath]\pm\sqrt{x}[/imath]. Thus, for example, the solution of [imath]x^2=4[/imath] consists of both roots, [imath]x=\pm\sqrt{4}=\pm2=2,-2[/imath]. Here we have to explicitly indicate that both signs are to be taken.

By the way, it is not "the principal of the square root", or "the square root principal"; "principal" means the primary, or main, root, the one we use by default. The principal square root of 4 is [imath]\sqrt{4}=2[/imath]; the other one has to be explicitly indicated as [imath]-\sqrt{4}=-2[/imath].

Good information for study notes. In terms of the word "principal", see attachment.