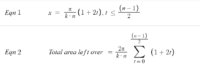DarkLink1994
New member
- Joined
- Jun 8, 2020
- Messages
- 4
Hi
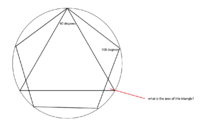
I am trying to calculate the left over area that the triangle makes with the pentagon which are both inscribed in a circle radius 1.
The interior angle of the triangle is 60 degrees and the interior angle of the pentagon is 108 degrees.
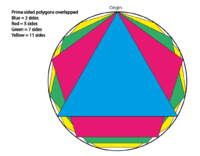
Please show how you work it out as I want to be able to apply this to n-sided inscribed polygons.
I am trying to calculate the left over area that the triangle makes with the pentagon which are both inscribed in a circle radius 1.
The interior angle of the triangle is 60 degrees and the interior angle of the pentagon is 108 degrees.
Please show how you work it out as I want to be able to apply this to n-sided inscribed polygons.