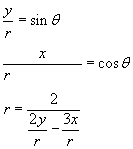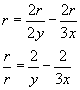polar equation to rectangular

[Shutterbug424]

[attachment=1:2u6d75mx]gunit.gif[/attachment:2u6d75mx]

[attachment=0:2u6d75mx]gunit2.gif[/attachment:2u6d75mx]

Should I have an r in my final answer?

I get 1 = (1/y) -(2/3x)

I don't know how to change that equation so the variables are on top.

 

[galactus]

Sub in \(\displaystyle r=\sqrt{x^{2}+y^{2}}\) into your final answer and simplify further.

 

[Deleted member 4993]

[attachment=1:2ewcwtzt]gunit.gif[/attachment:2ewcwtzt]

[attachment=0:2ewcwtzt]gunit2.gif[/attachment:2ewcwtzt]

Should I have an r in my final answer?

I get 1 = (1/y) -(2/3x) <<< How did you get that !! Show work.
I don't know how to change that equation so the variables are on top.

 

[Shutterbug424]

I realize this is probably wrong, but this is how I arrived at my answer:[attachment=0:dion7r03]gunit24.gif[/attachment:dion7r03]

 

[Deleted member 4993]

\(\displaystyle r \, = \, \frac{2}{\frac{2y}{r} - \frac{3x}{r}}\)

\(\displaystyle r \, = \, \frac{2r}{2y \, - \,3x}\)

Now continue.....

 

[Shutterbug424]

I factored out the r on the right side of the equation.

Then I divided the left side by r, giving me 1.

 

[Deleted member 4993]

Then what did you do....

 

[Shutterbug424]

That's where I'm stuck. I have no r left in my equation so I cannot substitute. My x and y are also in the denominator, which I cannot remedy.

 

[Shutterbug424]

Ok, now I understand why you kept pushing me forward slowly. I can't believe I did such sloppy algebra!

I got 2y- 3x = 2

I realize I cannot split the problem into 2 fractions. Silly me. Thanks.

 

[Deleted member 4993]

Now you got it.....