polar coordinates of the points of a circumference w.r.t. an inner point

[Maurilio]

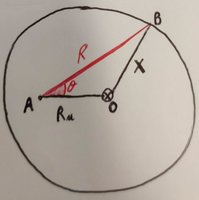
The question is how to find the relation between R and theta to characterize the function ''distance from the points of a circumference and an inner point''.
The circumference has radius X and the point is located at a distance Ru < X from the center of the circumference.
We want to find the polar coordinates (with respect to the inner point 'A') of the points 'B' of the circumference.

 

[HallsofIvy]

That's fairly straight-forward trigonometry. I assume that we are given points A and B and so know the angle inside the triangle at the center of the circle. I will call that "\(\displaystyle \phi\)".

By the "cosine law", \(\displaystyle R_A^2+ X^2= 2R cos(\phi)\) so that \(\displaystyle R= \frac{R_A^2+ X^2}{2 cos(\phi)}\). Then, by the "sine law", \(\displaystyle \frac{sin(\theta)}{X}= \frac{sin(\phi)}{R}\) so \(\displaystyle sin(\theta)= \frac{X}{R}sin(\phi)\).