Polar Coordinates-can someone check this please?

[pockystix]

hi,

I was doing a homework problem and need someone to check my work. My work seems to simple, so I think my answer is wrong...so I would appreciate it if someone can check it for me...Thanks in advance!

Here is the original problem:

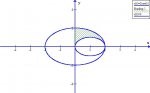
Show that the circle C with equation (x-1)^2 + y^2 = 1 has polar equation r = 2cos(theta). Using this and integration in polar coordinates find the area of the region bounded by the circle of radius 2 with center (0,0) outside C in the first quadrant.

My work:
http://img4.imageshack.us/img4/2273/hw1p.jpg

http://img4.imageshack.us/img4/7976/hw2i.jpg

 

[galactus]

\(\displaystyle (x-1)^{2}+y^{2}=1\)

\(\displaystyle x=rcos{\theta}, \;\ y=rsin{\theta}\)

\(\displaystyle (rcos{\theta}-1)^{2}+r^{2}sin^{2}{\theta}-1=0\)

\(\displaystyle r^{2}-2rcos{\theta}\)

\(\displaystyle r=2cos{\theta}\)

If we subtract the area of the upper half of C from the area in the first quadrant of the circle r=2, then we have the area outside C but inside the circle r=2.

\(\displaystyle \frac{1}{2}\int_{0}^{\frac{\pi}{2}}\left[4-(2cos({\theta}))^{2}\right]d{\theta}\)

You can also do it without calculus by just finding the areas of the two regions described and subtracting (area of circle formula). Do that to check your solution.

 

[pockystix]

i evaluated the integral and got pi/4 as my answer...Is that right? I tried doing the other method that you told me to check, but the answers were different...
Let me get this straight, all I have to do is find the area of the big circle and then subtract the area of the little circle right?
I got 4pi for the area of the big circle and pi for the little circle; 4pi - pi = 3pi not pi/4....

If you want, I can post my work to show you what I did...thanks

 

[galactus]

It is obviously not 4Pi. That is the area of the entire larger circle. Don't you need 1/4th that?. The portion in the first quadrant.

Area of larger circle in first quadrant. \(\displaystyle \frac{{\pi}(2)^{2}}{4}={\pi}\)

Area of upper half of C: \(\displaystyle \frac{{\pi}(1)^{2}}{2}=\frac{\pi}{2}\)

Subtract: \(\displaystyle {\pi}-\frac{\pi}{2}=\frac{\pi}{2}\)

Evaluate the integral and you will get the same thing (assuming it is done correctly).

 

[pockystix]

oopps. I forgot to divide the area by 4; I also looked over my integration and found out where I messed up. Thanks again galactus!