Points on a curve with vertical tangent lines

[corky0777]

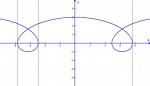
I am given a prolate cycloid graph defined by: x = 2t + 4 sin(t) and y = 2 + 4 cos(t) 0<=t<=2(pi) t=(pi)/4 (not sure if this is needed)

The problem says:
You should see four points on the curve with vertical tangent lines. Find the t-values of these four points, then the coordinates of the four points.

I have identified the tangent lines but do not know how to solve for the t-values and coordinates. Any help would be great

 

[corky0777]

Ok forget about the t= (pi)/4.... that was to a different part of the problem. sorry

 

[galactus]

Note that \(\displaystyle \frac{dx}{dy}=\frac{\frac{dx}{dt}}{\frac{dy}{dt}}\)

Find dx/dy, set to 0 and solve for t.

The solutions will be something like \(\displaystyle t=\frac{2(3C+1){\pi}}{3}, \;\ \frac{2(3C-1){\pi}}{3}\)

Try C values that satisfy the given interval. Plug these back into x and y above to find the coordinates of the vertical tangents.

The graph shows 3 of them.

 

[soroban]

Hello, corky0777!

Is that domain correct?
I found only two vertical tangents.

\(\displaystyle \text{Given a prolate cycloid: }\;\begin{Bmatrix}x &=& 2t + 4\sin t \\ y &=& 2 + 4\cos t \end{Bmatrix}\quad 0 \leq t \leq 2\pi\) .??

You should see four points on the curve with vertical tangent lines.
. . . . . . . . . . ?

(1) Find the \(\displaystyle t\)-values of these four points.

(2) Find the coordinates of the four points.

\(\displaystyle \frac{dy}{dx} \;=\;\frac{\frac{dy}{dt}}{\frac{dx}{dt}} \;=\;\frac{-4\sin t}{2 + 4\cos t}\)


. . \(\displaystyle \begin{array}{cccc}(a) & \text{Numerator} = 0: & \text{horizontal tangent} \\ (b) & \text{Denominator} = 0: & \text{vertical tangent} \end{array}\)


\(\displaystyle \text{We have: }\;(b)\;\;\underbrace{2 + 4\cos t}_{\text{This is }y} \;=\;0\)


\(\displaystyle \text{Since }y = 0\text{, the vertical tangents occur at the }x\text{-intercepts.}\)

. . \(\displaystyle 2 + 4\cos t \:=\:0 \quad\Rightarrow\quad \cos t \:=\:-\frac{1}{2} \quad\Rightarrow\quad t \;=\;\frac{2\pi}{3},\;\frac{4\pi}{3} \quad (1)\)


\(\displaystyle \begin{array}{ccccccc}t\:=\:\frac{2\pi}{3}: & x &=& 2(\frac{2\pi}{3}) + 4\sin\frac{2\pi}{3} &=& \frac{4\pi}{3} + 2\sqrt{3} \\ \\[-3mm] t\:=\:\frac{4\pi}{3}: & x &=& 2(\frac{4\pi}{3}) + 4\sin\frac{4\pi}{3} &=& \frac{8\pi}{3} - 2\sqrt{3} \end{array}\)


\(\displaystyle \text{Coordinates: }\;\left(\frac{4\pi}{3}+2\sqrt{3},\;0\right),\;\;\left(\frac{8\pi}{3} - 2\sqrt{3},\;0\right)\quad (2)\)