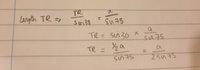Please help.. trig proof

[Jm23]

Can someone please help me on the attached question part ii - see pic.
I need to prove how sin 15 = 1/2 * sq root of (2 - sq root of 3). I have got as far as working out the angles of all the different triangles.

 

[Jm23]

This is what i have got so far..

 

[Deleted member 4993]

This is what i have got so far..

Have you learned Laws of Sines in a triangle?

 

[Jm23]

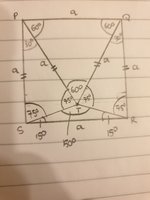
View attachment 17901View attachment 17900

Have you learned Laws of Sines in a triangle?

You mean the sine rule: a/sin A = b/ Sin B and vice versa for the angles?

 

[Deleted member 4993]

Yes - using that rule, and looking at the triangle QRT - can you express RT as a function of 'a'?

 

[Jm23]

Got this so far

 

[Deleted member 4993]

Got this so far

Now drop a perpendicular from T to SR - call it TR'.

drop a perpendicular from T to SR - call it TR'.

drop a perpendicular from T to PQ and call it TP'.

Calculate the length of TR' - using TR' = P'R' - P'T

and continue.....

 

[pka]

Can someone please help me on the attached question part ii - see pic.
I need to prove how sin 15 = 1/2 * sq root of (2 - sq root of 3). I have got as far as working out the angles of all the different triangles.

At the risk of confusing everything, I have a different take on this.
Consider \(M\) as the midpoint of \(\overline{PQ}~\&~N\) as the midpoint of \(\overline{RS}\).
Then \(M-T-N\) i.e. they are collinear. Because \(\Delta PQT\) equilateral the measure of \(\overline{MT} =\dfrac{a\sqrt 3}{2}\).
Moreover. the measure of \(\overline{MN} =a\) so the measure of \(\overline{TN} =a-\dfrac{a\sqrt 3}{2}\).
You should see some reasonable relations in all of this?

 

[Deleted member 4993]

At the risk of confusing everything, I have a different take on this.
Consider \(M\) as the midpoint of \(\overline{PQ}~\&~N\) as the midpoint of \(\overline{RS}\).
Then \(M-T-N\) i.e. they are collinear. Because \(\Delta PQT\) equilateral the measure of \(\overline{MT} =\dfrac{a\sqrt 3}{2}\).
Moreover. the measure of \(\overline{MN} =a\) so the measure of \(\overline{TN} =a-\dfrac{a\sqrt 3}{2}\).
You should see some reasonable relations in all of this?

It may be confusing sometimes - to discuss two different ways to do the same problem. However, I think that is an wonderful way to excerscize those little gray cells!!

Without that, how could we get more Hercule Poirot!!!