please help! domain, range, horizontal asymptote

M

mathplease

New member
Joined
Jul 16, 2009
Messages
4
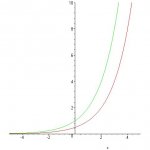
I don't know what the asnwer should be... i need to find the domain, range, and horizontal asymptote of a transformed graph. f(x)=2^x ---> g(x)2^(x-1)
and put (-infinity,infinity) for domain and range, but now i'm thinking that the range is only positive numbers, so how would i write that? [0,infinity) ???? Do i need a bracket or parenthesis?
and for the horizontal asymptote i put 1, but i really don't know.
 
If you look at the graph, it should be obvious that the domain is (-?,?), the range is (0,?) and the horizontal asymptote is y=0.

[attachment=0:1ozscpy5]eee.jpg[/attachment:1ozscpy5]

The green line is y = 2^x and the red line is y = 2^(x-1).
 

Attachments

  • eee.jpg
    eee.jpg
    16 KB · Views: 169
i just don't understand it... how do you when to put brackets by the number? how come there is a parenthesis instead of bracket next to the zero? and i don't get the asymptotes either...
 
Either you are pulling my chain, or else you need to start attending class and/or start cracking your book on Calc., instead of staying out all night at the local disco doing the boogaloo.

Note: This is a calculus thread, the above should be second nature to you if you are now enroled in a calculus class.
 
mathplease said:
i just don't understand it... how do you when to put brackets by the number? how come there is a parenthesis instead of bracket next to the zero? and i don't get the asymptotes either...
Click to expand...
This should be like algebra or w.e

Anyways I believe [ means inclusive and ( means exclusive. So if x is an element of [0, 5) then it means x is greater than or equal to 0 and less than (not equal to) 5. Another way of writing domain/range would be:

\(\displaystyle \[\begin{array}{l} D = \{ x|x \in R, - \infty < x < \infty \} \\ R = \{ y|y \in R,0 < y < \infty \} \\ \end{array}\]\)
 
Right on fred2028, but what you are saying is Algebra 101, not "The Calculus".

To be blunt, I think we were being "had" by Mathplease.
 
You must log in or register to reply here.
Top