Please help! Counting Methods/Probability Outcome Problem

[Sharnice]

I'm really stuck on this problem. I wrote in my own little notes on the side but I just cant seem to understand how to put this is a product table. I know how to do it with just the two regular 6 sided dice, but not this one. Any help is greatly appreciated!!

 

[Steven G]

One can only assume that the four sided die has 1, 2, 3 and 4 on it and that the eight sided die has 1 through 8 on it (??).
What exactly do you mean by a product table? Do you just the fine score, the probabilities or the number of outcomes?
If you want the final score then for example a roll of a 3 followed by a 7 would put a 21 in that square while a roll of a 4 followed by a 1 would put a 5 in that square

 

[JeffM]

The problem is not well worded. A problem easily worked around is the singular is "die" rather than ":dice." Not so easily worked around is that what is on each face of each die is not explicitly specified. Even weirder, the four-sided die appears to show three different numbers. What determines the "number" of the four-sided die is not specified.

I am going to guess from the picture shown that, on each face of the four-sided die, three of the numbers from 1 through 4 are shown, a single number at each apex. One side does not show 1; another does not show 2; a third does not show 3, and the last does not show 4. I have no guess on which number is chosen from the three faces showing. I am guessing from the picture that each face of the 8-sided die contains a single number from 1 through 8 and that there is no ambiguity about which face is on top.

 

[Sharnice]

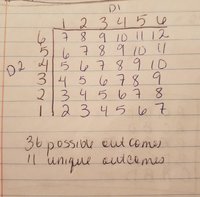
@JeffM and @Jomo The Example given to us in class was the much simpler one (using two regular 6 sided dice) that I've attached to this message. The easier example also defines what the product table is. I'm supposed to find the possible outcomes and construct a similar table. I believe that I'm getting confused because of the different possibilities for each answer. It seems unknown because what if John rolled an odd number on the first and second dice, or vice versa. I apologize for my lack of being able to explain any better than this.

 

[Romsek]

Roll 4 sided die 1 to obtain $\displaystyle r \in \{1,2,3,4\}$
Roll 8 sided die 2 to obtain $\displaystyle s \in \{1,2,3,4,5,6,7,8\}$

$\displaystyle output =\begin{cases}r\cdot s &r \text{ is odd}\\r + s &r \text{ is even}\end{cases}$

Spoiler

 

[pka]

According to the description the outcome space is a set of pairs $\displaystyle (x,y)$ where $\displaystyle 1\le x\le y~\&~1\le y\le 8$.
Then we get $\displaystyle \text{result }=xy\text{ if }x\text{ is odd}$ OR $\displaystyle \text{result }=x+y\text{ if }x\text{ is even}$.
Now if the result is $\displaystyle 6$ then the pairs could be $\displaystyle (1,6),~(2,4),~(3,2),~\text{ or }~(4,2)$
But the probability of any pair is $\displaystyle \frac{1}{32}$