pipeline word problem

[dear2009]

Hey everybody,



I am trying to solve this word problem through the derivative but I cant seem to get the right answer even though I did the right method

Here is the problem
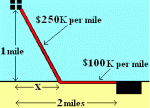
The task is to construct the minimum-cost pipeline from an offshore platform to an onshore refinery. The refinery is located 10 miles up the coast from the platform, and the platform is located 2 miles off the coast, as shown in the diagram below. Assuming it costs $18K per mile to build the pipeline on the land, and $30K per mile to construct the pipeline offshore, what is the minimum cost for the project?

Here is what I did

(square root of 4 + x^2)(30 + (2 - x) 18))
(square root of 4 + x^2)(30 + 36 - 18x)
C'(x) = 0
C ' (x) = 1/2 (4 + x^2)^ -1/2 (2x) (30) - 18
(30x) /( square root of 4 + x^2) - 18 = 0
(30x) /( square root of 4 + x^2) = 18

I eventually got 25x^2/9 = 4 + x^2
x = 3/2

25x^2 - 9x^2 / 9 = 4

when I plugged this in to the (square root of 4 + x^2)(30 + (2 - x) 18))
I got 84 (from 75 + 9, on the last step of plugging in)
but the answer is supposed be around 228-233

Can anybody help me?

 

[galactus]

The diagram you have appears to have different costs than what is in the problem statement.

The cost on land is \(\displaystyle 18(10-x)\)

The cost underwater is \(\displaystyle 30\sqrt{x^{2}+4}\)

Total cost is \(\displaystyle 18(10-x)+30\sqrt{x^{2}+4}\)

Differentiate and get \(\displaystyle \frac{dC}{dx}=\frac{30x}{\sqrt{x^{2}+4}}-18\)

Set to 0 and solve for x: \(\displaystyle \frac{30x}{\sqrt{x^{2}+4}}-18=0\)

\(\displaystyle \frac{30x}{\sqrt{x^{2}-4}}-18\cdot\frac{\sqrt{x^{2}+4}}{\sqrt{x^{2}+4}}=0\)

\(\displaystyle 30x=18\sqrt{x^{2}+4}\)

Square both sides and simplify:

\(\displaystyle 576x^{2}=1296\)

\(\displaystyle x=\frac{3}{2}\)

Plug this back into the total cost formula and get C=228