Parabola Intersection Problem

[turophile]

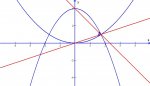
Here's the problem:

Lines are drawn from a point of intersection of the parabolas y = ax[sup:2o8005mv]2[/sup:2o8005mv] and y = 4 – x[sup:2o8005mv]2[/sup:2o8005mv] to the vertex of each parabola. For what value of a are these lines perpendicular?

Here's what I've done so far:

Let P = (u, v) be a point of intersection. Since v = au[sup:2o8005mv]2[/sup:2o8005mv], P = (u, au[sup:2o8005mv]2[/sup:2o8005mv]). Let m[sub:2o8005mv]1[/sub:2o8005mv] be the slope of the line through P and the vertex of parabola y = ax[sup:2o8005mv]2[/sup:2o8005mv], (0, 0), and let m[sub:2o8005mv]2[/sub:2o8005mv] be the slope of the line through P and the vertex of parabola y = 4 – x[sup:2o8005mv]2[/sup:2o8005mv], (0, 4). Then m[sub:2o8005mv]1[/sub:2o8005mv] = (au[sup:2o8005mv]2[/sup:2o8005mv] – 0) / (u – 0) = au, and m[sub:2o8005mv]2[/sub:2o8005mv] = (au[sup:2o8005mv]2[/sup:2o8005mv] – 4) / (u – 0) = au – 4 / u. We want m[sub:2o8005mv]1[/sub:2o8005mv] = – 1 / m[sub:2o8005mv]2[/sub:2o8005mv] for the lines to be perpendicular.

? au = – 1 / (au – 4 / u)

? au(au – 4 / u) + 1 = 0

? a[sup:2o8005mv]2[/sup:2o8005mv]u[sup:2o8005mv]2[/sup:2o8005mv] – 4a + 1 = 0

At this point, I need to substitute a value for u[sup:2o8005mv]2[/sup:2o8005mv] in order to solve for a, but I'm not sure how to find that value.

 

[galactus]

Here is a way I worked out. I am sure there are more.

Since you give things an earnest effort.

\(\displaystyle y=4-x^{2}\) has vertex at (0,4) and \(\displaystyle y=ax^{2}\) has vertex at (0,0).

Let \(\displaystyle (p, \;\ 4-p^{2})\) be a point on the parabola \(\displaystyle y=4-x^{2}\)

It's slope from (0,4) is \(\displaystyle m_{1}=\frac{4-(4-p^{2})}{-p}=-p\)

The slope from the origin is \(\displaystyle m_{2}=\frac{4-p^{2}}{p}\)

Multiply them, and to be perpendicular the product should be -1.

\(\displaystyle -p\left(\frac{4-p^{2}}{p}\right)=p^{2}-4\)

\(\displaystyle p^{2}-4=-1\Rightarrow p=\pm\sqrt{3}\)

But, the two parabolas intersect at \(\displaystyle 4-p^{2}=ap^{2}\Rightarrow p=\frac{2}{\sqrt{a+1}}\)

\(\displaystyle \frac{2}{\sqrt{a+1}}=\sqrt{3}\)

\(\displaystyle a=\frac{1}{3}\)

The parabola has equation \(\displaystyle \boxed{y=\frac{1}{3}x^{2}}\)

They may not look perpendicular on the graph, but they are.