Overall Dimensions

R

Ryan Rigdon

Junior Member
Joined
Jun 10, 2010
Messages
246
Here is my next problem.

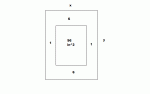
Johnny is designing a rectangular poster to contain 96in^2 of printing with a 6-in margin at the top and bottom and a 1-in margin at each side. What overall dimensions will minimize the amount of paper used?

The dimensions of the poster that minimize the amount of paper used are ____ in.
(Simplify your answers. Use a comma to separate answers.)

Work to follow soon.
 
how could i post a drawing of this. the only program i have is Mathematica 7. I just want to get it done as fast as possible rather than spending 3 or 4 hours on it.
 
Make a drawing in Paint and save it to your computer. Then, use the Upload Attachments at the bottom of the page to load the file onto the site.

The area of the whole page is A=xy

Now, try to express the area of the printed portion and set it equal to 96. Solve for y and sub into the area formula.

See, these problems are all based on the same theme. Whittle down to one variable, differentiate, set to 0 and solve for blah, blah, blah

Like so:
 

Attachments

  • print.gif
    print.gif
    3.4 KB · Views: 144
galactus said:
Make a drawing in Paint and save it to your computer. Then, use the Upload Attachments at the bottom of the page to load the file onto the site.

The area of the whole page is A=xy

Now, try to express the area of the printed portion and set it equal to 96. Solve for y and sub into the area formula.

See, these problems are all based on the same theme. Whittle down to one variable, differentiate, set to 0 and solve for blah, blah, blah

Like so:
Click to expand...


When you ask try to express the area of the printed portion and set it equal to 96? Does the following look right so far?

2x + 2y - (2(6x + 1y)) = 96
 
Ryan Rigdon said:
galactus said:
Make a drawing in Paint and save it to your computer. Then, use the Upload Attachments at the bottom of the page to load the file onto the site.

The area of the whole page is A=xy

Now, try to express the area of the printed portion and set it equal to 96. Solve for y and sub into the area formula.

See, these problems are all based on the same theme. Whittle down to one variable, differentiate, set to 0 and solve for blah, blah, blah

Like so:
Click to expand...


When you ask try to express the area of the printed portion and set it equal to 96? Does the following look right so far?

2x + 2y - (2(6x + 1y)) = 96
Click to expand...

Expression of area involves multiplication....
 
Subhotosh Khan said:
[quote="Ryan Rigdon":1hc3c5ow]
galactus said:
Make a drawing in Paint and save it to your computer. Then, use the Upload Attachments at the bottom of the page to load the file onto the site.

The area of the whole page is A=xy

Now, try to express the area of the printed portion and set it equal to 96. Solve for y and sub into the area formula.

See, these problems are all based on the same theme. Whittle down to one variable, differentiate, set to 0 and solve for blah, blah, blah

Like so:
Click to expand...


When you ask try to express the area of the printed portion and set it equal to 96? Does the following look right so far?

2x + 2y - (2(6x + 1y)) = 96
Click to expand...

Expression of area involves multiplication....[/quote:1hc3c5ow]


i have tried two different ways

one way

6xy = 96

another way

2(6x)+2(y) = 96

both of which i think are wrong but i am leaning towards 2(6x)+2(y) = 96
 
Ryan Rigdon said:
[quote="Subhotosh Khan":12ce3ls9]Please define 'x' and 'y'.
Click to expand...


x = 6 in margin and y = 1 in margin[/quote:12ce3ls9]

So according to you 'x' and 'y' are already known - why are you calling those 'x' and 'y' (which are generally reserved for calling unknown parameters)?

and you wrote:

2(6x)+2(y) = 96

Putting values of x and y into left-hand-side, we get,

2(6*6) + 2*1

= 72 +2

= 74

We don't get your proposed right-hand-side.
 
i have no idea. i am just lost and confused and i am getting nowhere with this problem. i want to know how to do because I need to.

is it possible to give me an example of a problem like this one that has been completed on a separate post or something.
 
Subhotosh Khan said:
[quote="Ryan Rigdon":ksrnjl6q]
galactus said:
Make a drawing in Paint and save it to your computer. Then, use the Upload Attachments at the bottom of the page to load the file onto the site.

The area of the whole page is A=xy

Now, try to express the area of the printed portion and set it equal to 96. Solve for y and sub into the area formula.

See, these problems are all based on the same theme. Whittle down to one variable, differentiate, set to 0 and solve for blah, blah, blah

Like so:
Click to expand...


When you ask try to express the area of the printed portion and set it equal to 96? Does the following look right so far?

2x + 2y - (2(6x + 1y)) = 96
Click to expand...

Expression of area involves multiplication....[/quote:ksrnjl6q]


I know the area from the inside rectangle is suppost to be subtracted from the outside rectangle. i just cant figure out how to express it.
 
You know that the area of the whole thing is A=xy

The width of the page is x and the length y, so wouldn't the width of the printed region be x-2, because there is 1" on each side?.

The length would be y-12, because there is a 6' margin on the top and bottom?.

Then, wouldn't the area of the printed region be (x-2)(y-12)?. See why that is?. Look at the diagram I posted earlier.
 
galactus said:
You know that the area of the whole thing is A=xy

The width of the page is x and the length y, so wouldn't the width of the printed region be x-2, because there is 1" on each side?.

The length would be y-12, because there is a 6' margin on the top and bottom?.

Then, wouldn't the area of the printed region be (x-2)(y-12)?. See why that is?. Look at the diagram I posted earlier.
Click to expand...


Now that i look at it again after a long rest. width is x and length is y.

the width of printed region be x - 12, there is 6" on each side

length would be y - 2, there is 1" on each side. so the area of the printed region is (x-12)(y-2).

(x-12)(y-2) = 96

xy - 2x - 12y = 96

xy - 12y = 2x + 96

y(x - 12) = 2x + 96

y = (2x + 96)/(x - 12)

Plug into A = xy

x((2x + 96)/(x - 12))

= (2x^2 + 96x)/(x-12)

looking better?
 
\(\displaystyle Let \ xy \ = \ 96, \ printed \ area.\)

\(\displaystyle Then \ (x+2)(y+12) \ = \ Total \ Area \ of \ poster.\)

\(\displaystyle Hence \ Total \ Area \ = \ xy+12x+2y+24 \ = \ 96+12x+\frac{192}{x}+24\)

\(\displaystyle Ergo, \ A \ = \ 12x+\frac{192}{x}+120, \ xy \ = \ 96 \ and \ y \ = \ \frac{96}{x}\)

\(\displaystyle Hence, \ \frac{dA}{dx} \ = \ 12-\frac{192}{x^2} \ = \ 0 \ \implies \ x \ = \ 4.\)

\(\displaystyle When \ x \ =4, \ y \ = \ 24, \ (4)(24) \ = \ 96\)

\(\displaystyle Therefore, \ total \ dimensions \ of \ poster \ = \ (x+2)(y+12) \ = \ 6 \ X \ 36, \ skinny.\)

\(\displaystyle See \ graph \ below \ for \ min.\)

[attachment=0:21r7daii]eee.jpg[/attachment:21r7daii]
 

Attachments

  • eee.jpg
    eee.jpg
    12 KB · Views: 23
i was almost there. thanx for working it out for me. means a lot. i wanted to do it myself but you know sometimes everyone needs help. thanx again. :D


this is the part i had trouble getting, would you mind explaining it a little more.

\(\displaystyle Then \ (x+2)(y+12) \ = \ Total \ Area \ of \ poster.\)
 
\(\displaystyle Ryan, \ I \ don't \ know \ how \ I \ can \ be \ any \ more \ succinct \ than \ I \ been.\)

\(\displaystyle Just \ pore \ over \ slowly \ and \ you \ should \ get \ it.\)
 
Therefore,

The dimensions of the poster that minimize the amount of paper used are 6x36 in.
 
Yes. Glenn used x and y as the width of the printed region, whereas SK and I used x and y as the width and length of the paper.

Either way will result in the same solution.

I may as well go ahead and show the other method. It is very similar, and you always give an earnest effort.

The area of the whole paper is \(\displaystyle A=xy\)

The area of the printed region is then \(\displaystyle (x-2)(y-12)=96\)

Now,here you expanded out and made things a little harder than need be. What you done is OK, but not as efficient.

merely divide by x-2:

\(\displaystyle y-12=\frac{96}{x-2}\)

Add 12:

\(\displaystyle y=\frac{96}{x-2}+12\).....................[1]

Sub into A=xy:

\(\displaystyle x\left(\frac{96}{x-2}+12\right)=\frac{12x(x+6)}{x-2}\)

Differentiate:

\(\displaystyle A_{p}(x)=\frac{12(x^{2}-4x-12)}{(x-2)^{2}}\)

Set to 0 and solve for x. But all we have to do is solve the quadratic in the parentheses.

\(\displaystyle x^{2}-4x-12=(x-6)(x+2)\)

\(\displaystyle \fbox{x=6, \;\ x=-2}\)

Of course, -2 is extraneous, so we go with x=6

Therefore, the width of the entire sheet is x=6.

The height, y, can be found by subbing into [1]:

\(\displaystyle \frac{96}{6-2}+12=36\)

The dimensions of the entire sheet are 36 by 6.

There are most always more than one way to tackle these problems. Also, keep in mind that these problems are very cliche. They are used over
and over in calc texts. Do you see the theme to tackling these optimization problems?. They all have pretty much the same modus operandi in solving them. Find what you are optimizing and write a formula; Solve the other formula for a variable and sub into the one being optimized so you have one variable to deal with; differentiate, etc, etc.

One of my favorites is 'carrying the pipe around a corner'. In this one, a pipe is carried around a 90 degree corner from one hallway into another with the hallways being of different widths. The task is to find the pipe of max length that will fit around the corner. You will probably run into this one. Look in your book and I bet it's in there. The width of the pipe is not taken into account. If it were, the problem is much more difficult.
 
You must log in or register to reply here.
Top