Optimum Straight Line: calculating 'best fit' for points

T

ttibsen

New member
Joined
Jul 17, 2006
Messages
3
I was uncertain in which category this question belongs so bear with me if this perhaps was not the right place in which to post. Anyway - here is my question -

If you have a bunch of points on an XY graph - how do you calculate the straight line Y = mX + B that is the best fit through those points? In fact, what do you call such a line? I remember all this vaguely from high school but now I actually have the need to do these calculations.

Thanks

John Stern
 
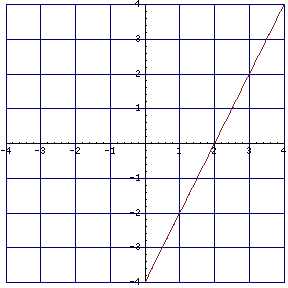
To find the straight line: \(\displaystyle \L y=mx+b\)

If you have a graph of a line like this:
Line-1.+0.-2.-2.gif

\(\displaystyle \L y=mx+b\)

To find the \(\displaystyle m\)(slope) you pick any two points on the line and and subtract the y's and the x's w/the subtraction of the y-coordinates on top andsubtraction of the x-coordinates ont the bottom.

So I will pick an two points to find our slope: \(\displaystyle \L (2,0)(1,-2)= \frac{0-(-2)}{2-1}=\frac{2}{1}\to2\)

So our equation is \(\displaystyle \L y=2x+b\)

Now to find the y-intercept \(\displaystyle \L b\) by filling any coordinate on the line:

\(\displaystyle \L 0=2(2)+b\)

\(\displaystyle \L 0=4+b\)

\(\displaystyle \L -4=b\)

So our equation is \(\displaystyle \L y=2x-4\)

If you fill in any coordinate \(\displaystyle \L y\) or \(\displaystyle \L x\) you will always get the other coordinate.

To find the line of best fit
One of the simplest things you can do is to find the slope between
each adjacent set of points.If you do this for the other pairs, you'll get a collection of slopes, and you could take the average of these.

Another thing you can do is plot the points on graph paper, and use a
ruler to draw the line that seems to go through the 'middle' of the
points, i.e., so that some of the points are above the line, while
others are below.

On the other hand, if this represents real data that someone really
cares about, you'd want to do something more sophisticated, like a
least-squares analysis. This has the same effect as finding the line
such that the sum of the squares of the distances from each point to
the line is minimized, which is one way of defining 'best'.

http://mathforum.org/library/drmath/view/63337.html
 
You want a linear regression.

I would use a calculator, but if you must do it the 'old-fashioned' way here are some formulae using yur data points.

Slope m=\(\displaystyle \L\\\frac{n\sum{xy}-(\sum{x})(\sum{y})}{n\sum{x^{2}}-(\sum{x})^{2}}\)

b=\(\displaystyle \L\\\frac{\sum{y}}{n}-m\frac{\sum{x}}{n}\)
 
I see good guesses, but in reality you must define what you mean by "best fit". I have little doubt that galactus is right on, but you really should provide a definition. The least squares version shown is one popular methodology.
 
You must log in or register to reply here.
Top