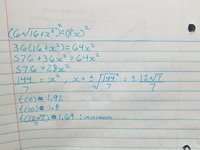A person in a boat 4km off the coast. The person needs to reach a point 10km down and along the coast in the least possible time. The person can row 6km/hr and run 8km/hr. How far down the coast should he land the boat.
I know how to solve this using calculus. I create a function of time, take the derivative and set it equal to zero, and then solve for x. Then I check the critical points to find the minimum. However, my professor wants me to try and solve it only using trigonometry and not calculus. I tried a could of things, such as creating a function for time, where the angle theta is the input variable, but after that I was just plugging in values to try and find the optimal angle theta and then eventually solving for x.
Thank you
I know how to solve this using calculus. I create a function of time, take the derivative and set it equal to zero, and then solve for x. Then I check the critical points to find the minimum. However, my professor wants me to try and solve it only using trigonometry and not calculus. I tried a could of things, such as creating a function for time, where the angle theta is the input variable, but after that I was just plugging in values to try and find the optimal angle theta and then eventually solving for x.
Thank you