Optimization Problem

[asimon2005]

4. Find a positive number such that the sum of the number and its reciprocal is as small as possible.

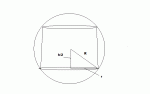
29. A right circular cylinder is inscribed in a sphere of radius r. Find the largest possible surface ares of such a cylinder.

 

[daon]

Well, if 0 < a <= 1 then a+1/a >= 1+a.

Note if a=1, then we get a+1/a = 2. Therfore we are looking for a such that a+1/a < 2. Are there any?

 

[galactus]

29. A right circular cylinder is inscribed in a sphere of radius r. Find the largest possible surface ares of such a cylinder.

Let R be the radius of the sphere and r be the radius of the cylinder. Also, h is the height of the cylinder.


\(\displaystyle S=2{\pi}rh+2{\pi}r^{2}\)

But, \(\displaystyle r^{2}+(\frac{h}{2})^{2}=R^{2}\)

\(\displaystyle h=2\sqrt{R^{2}-r^{2}}\)

\(\displaystyle S=4{\pi}r\sqrt{R^{2}-r^{2}}+2{\pi}r^{2}\)

This is what should be optimized by finding dS/dr. Remember, R is a constant.