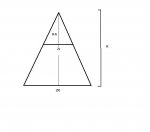
Find the maximum volume of a right-circular cone placed upside-down in a right-circular cone of radius R and height H.
http://img451.imageshack.us/i/optimizationfi3.jpg/
All I understand is that if you view the image in profile view, you have two similar triangles...I have no idea where to go from that.
[attachment=0:1xdx6m0q]triangle.jpg[/attachment:1xdx6m0q]
http://img451.imageshack.us/i/optimizationfi3.jpg/
All I understand is that if you view the image in profile view, you have two similar triangles...I have no idea where to go from that.
[attachment=0:1xdx6m0q]triangle.jpg[/attachment:1xdx6m0q]