Optimization? i think?

[rafeeki92]

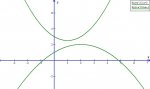
Suppose that the position of function of two particles, P1 and P2 in motion on along the same line are:
S1 = .5t^2 - t + 3
and
S2 = -.25t^2 + t + 1

How close can P1 and P2 get to one another?



Ok..so Ive proven that P1 and P2 never collide, but I'm not sure how to derive the minimum distance between the two functions on a graph...help please

 

[galactus]

Graph the two functions. They are parabolas that come close to one another.

Subtract the two quadratics, find the derivative of the quadratic obtained, set to 0 and solve for t.

Sub that t value back into the quadratic resulting from the subtraction of the two given quadratics to find the minimum distance.

 

[chrisr]

Hi Rafeeki92,

you probably calculated S[sub:2ojre8iq]1[/sub:2ojre8iq]-S[sub:2ojre8iq]2[/sub:2ojre8iq] and rewrote it as 3t[sup:2ojre8iq]2[/sup:2ojre8iq]-8t+8=0.
You don't have to, you may leave it at 0.75t[sup:2ojre8iq]2[/sup:2ojre8iq]-2t+2.
S[sub:2ojre8iq]1[/sub:2ojre8iq] cannot equal S[sub:2ojre8iq]2[/sub:2ojre8iq] as the resulting equation does not have real roots.

To find the minimum value of S[sub:2ojre8iq]1[/sub:2ojre8iq]-S[sub:2ojre8iq]2[/sub:2ojre8iq], you differentiate the above with respect to t.
Notice that it is a parabola with a minimum (S[sub:2ojre8iq]2[/sub:2ojre8iq]-S[sub:2ojre8iq]1[/sub:2ojre8iq] would have inverted the graph).

When you equate the derivative to zero, you are discovering the time "t", corresponding to minimum distance.
You will have to place that t back into the resulting quadratic which expresses the distance between the particles.

Distance between them = position[sub:2ojre8iq]1[/sub:2ojre8iq] - position[sub:2ojre8iq]2[/sub:2ojre8iq].
Minimum distance = 0.75(t[sub:2ojre8iq]min[/sub:2ojre8iq])[sup:2ojre8iq]2[/sup:2ojre8iq]-2t[sub:2ojre8iq]min[/sub:2ojre8iq]+2

 

[rafeeki92]

ok...my question is WHY do we find the differences of the functions? that confuses me a bit

 

[galactus]

Look at the graph. Intuitively, wouldn't you need to subtract in order to find the difference between the points on the repective graphs?.

By differentiating, we find the optimum distance. In this case, the minimum.

 

[BigGlenntheHeavy]

\(\displaystyle If \ they \ collide, \ then \ s_1 \ = \ s_2, \ so \ \frac{t^{2}}{2}-t+3 \ = \ -\frac{t^{2}}{4}+t+1, \ \frac{3}{4}t^{2}-2t+2 \ = \ 0 \ which \ has \ no \ real\)

\(\displaystyle \ solution, \ (they \ don't \ collide).\)

\(\displaystyle Let \ D \ = \ the \ distance \ between \ s_1 \ and \ s_2, \ then \ D(t) \ = \ |s_1-s_2| \ = \ |\frac{3}{4}t^{2}-2t+2|.\)

\(\displaystyle From \ above \ D(t) \ is \ never \ zero, \ and \ for \ t \ = \ 0 \ it \ is \ positive, \ hence \ it \ is \ always \ positive, \ so \ D(t ) \ =\)

\(\displaystyle \ \frac{3}{4}t^{2}-2t+2, \ \frac{dD}{dt} \ = \ \frac{3}{2}t-2 \ = \ 0 \ when \ t \ = \ \frac{4}{3}.\)

\(\displaystyle \frac{d^{2}D}{dt^{2}} \ > \ 0 \ so \ D \ is \ minimum \ when \ t \ = \ \frac{4}{3}, \ D(4/3) \ = \ \frac{2}{3} \ = \ min. \ distance \ between \ the \ two \ points.\)