Optimization: given 2000 sq ft, 5 pens, find min. fencing

[thatguy47]

Problem: Minimize amount of fence required to pen 5 animals separately. The total area available is 2000 square feet.

I know that the answer is 3010 ft and the w=25.820 l=76.46 but I cant figure out how this is solved. I started out by drawing a picture that was 6 x 2 but I couldn't figure out what to do from there. Please help me with this. Thanks.

 

[mmm4444bot]

Re: Optimization / Minimize Problem

I know that the answer is 3010 ft ...

Hi Guy:

Your answer is way off. Did you forget a decimal point, or did somebody give you the wrong answer? (301.0 ft is also incorrect, but that number is only off by about nine feet, or so.)

Also, the exercise, as you typed it, is not worded very clearly. I've read it as follows.

"Five adjacent rectangular pens of equal dimension are to be constructed such that their aggregate area is 2,000 square feet and a minimum amount of fencing is used. How many feet of fence will be required?"

You drew a 6×2 picture. I'm not sure what this picture looks like. Six by two what? Are these the dimensions of the media on which you drew it? (Just kidding ...)

I drew a picture. (Excuse the sloppiness; my scanner stopped working, so I had to use MSPaint. The five pens are supposed to have equal areas.)

[attachment=0:218viquu]junk932.JPG[/attachment:218viquu]

Does this look similar to your picture?

\(\displaystyle (5x) \cdot w = 2000\)

Use this equation to express w in terms of x.

Write an expression that represents the sum of all the Ws and Xs needed to construct these pens. Such an expression represents the total length of fencing.

Substitute the expression for w that you found above into the expression that you wrote for the total length of fencing.

You now have a function in terms of x. To find the minimum value of this function, calculate its derivative function, and seek the value of x at which the derivative is zero.

Once you know this value of x, you can find the corresponding w. From there, it's "easy street".

Please show your work, if you need more help, and try to say something about why you're stuck.

Cheers,

~ Mark

PS: When you report your final answer for the total amount of fencing required, round it off to only one decimal point. Nobody is going to measure fencing to the nearest hundredth or thousandth of a foot.

 

[TchrWill]

Minimize amount of fence required to pen 5 animals separately. The total area available is 2000 square feet.

I know that the answer is 3010 ft and the w=25.820 l=76.46 but I cant figure out how this is solved. I started out by drawing a picture that was 6 x 2 but I couldn't figure out what to do from there. Please help me with this. Thanks.

*--Considering all rectangles with the same perimeter, the square encloses the greatest area.
Proof: Consider a square of dimensions x by x, the area of which is x^2. Adjusting the dimensions by adding a to one side and subtracting a from the other side results in an area of (x + a)(x - a) = x^2 - a^2. Thus, however small the dimension "a" is, the area of the modified rectangle is always less than the square of area x^2.

*--Considering all rectangles with the same area, the square results in the smallest perimeter for a given area.

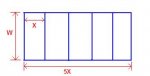
Consider 5 squares with sides "x", 4 clusterd together to form a larger square "2x" by "2x", and 1 "x" by "x" square attached to any one of the 8 sides of the smaller squares.

There are 10 external edges and 5 common internal edges for 15 edges in all forming 5 pens.

The enclosed area of the 5 pens is 5x^2 = 2000 making x = 20 ft.

The total length of fencing is therefore 15(20) = 300 ft.

 

[Loren]

Your problem leaves much to be desired. It does not stipulate that the pens are all to be of the same size. Nor, does it say that they should all be side by side. Please clarify.

 

[TchrWill]

Problem: Minimize amount of fence required to pen 5 animals separately. The total area available is 2000 square feet.

I know that the answer is 3010 ft and the w=25.820 l=76.46 but I cant figure out how this is solved. I started out by drawing a picture that was 6 x 2 but I couldn't figure out what to do from there. Please help me with this. Thanks.

You might want to explore one large square pen with a smaller square pen in the center with all 8 vertices attached by 4 edges.

The sum of the 4 trapazoidal pens plus the smaller internal square pen is 2000 sq.ft. The area of each of the 5 pens could be equal or not equal. Optimizing for minimum fence length would be worth exploring.

If one considered unequal pen sizes, such as one large square with 4 internal sides made by joining the mid points of the larger outer square, results in a fence length of 305 ft.

There are any number of pen configurations that would satisfy the area requirement depending on the relative pen sizes.

 

[wjm11]

Actually, two concentric circles with four dividers in the torus would be most efficient, I'm guessing.

 

[mmm4444bot]

Your problem leaves much to be desired. It does not stipulate that the pens are all to be of the same size. Nor, does it say that they should all be side by side. Please clarify.

Hello Guy:

Your exercise also does not state that the entire available area needs to be used ... what kind of animals are you trying to pen?

~ Mark :|

 

[TchrWill]

Actually, two concentric circles with four dividers in the torus would be most efficient, I'm guessing.

Then, A = PiR^2 - Pir^2 = 2000.
The limiting case of this would be when r = 0 yielding a circle of R = 25.231.

Adding 5 dividers of length 25.231, the perimeter (or length of fencing required) would then be Pi(25.231)2 + 5(25.231) = 158.5 + 126.15 = 284.7 ft.