HATLEY1997
Junior Member
- Joined
- Oct 24, 2023
- Messages
- 59
How are you getting that value of the horizontal leg?For part (a), refer to the 3D diagram.
Note the right triangle with hypotenuse R, vertical leg y/2, and horizontal leg [imath]\dfrac{\sqrt{2}}{2} \cdot x[/imath]
How are you getting that value of the horizontal leg?
I have used Pythagoras and 2r as the hypotenuse, with the vertical leg as y and the horizontal leg as x, however when rearranging this equation I am getting x^2=2r^2-y^2. Where am I getting the (1/2)y^2 from?
This may help:How are you getting that value of the horizontal leg?
I have used Pythagoras and 2r as the hypotenuse, with the vertical leg as y and the horizontal leg as x, however when rearranging this equation I am getting x^2=2r^2-y^2. Where am I getting the (1/2)y^2 from?
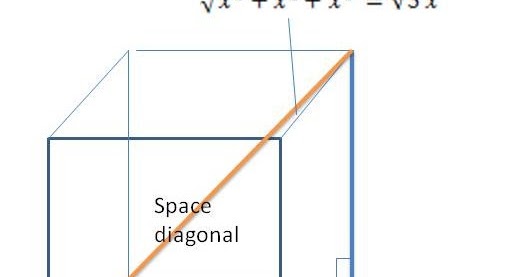
I think part of the confusion may be that this image is not through diagonally opposite edges, but through the front face:Look at the cross-section by a vertical plane which contains two diagonally opposite vertical edges of the cuboid.
Yes, this would be one way to do it. @skeeter is doing something similar, but working only with R, from the center to a vertex, rather than with the whole cuboid and diagonal/diameter 2R.I think I know what I have been doing wrong and it’s by using the x as the horizontal leg. Should I be using the formula xsqrt(2)?
You have V in terms of R and y. But R is a constant, not a variable. It shouldn't get in the way.I understand my first step for part c is finding the derivative, however having both the r and y variables is throwing me off finding the stationary points, any advice?
Yes, except that y can't be negative.Thank you!
Am I right in thinking the stationary points are 2r/sqrt(3) and -2r/sqrt(3)?
Thank you! To show that this is the maximum, should I use 2nd derivative test?Yes, except that y can't be negative.
And R is uppercase. In math, that is often significant (e.g. R and r might mean outer and inner radii), so you should develop the habit of using variables exactly as given!
To apply the second derivative test, you just need to find the second derivative (which is not yet correct!), and then put your value for y into the formula for the second derivative. It will be obvious whether it is negative! (It will simplify to a numerical multiple of R.)Thank you! To show that this is the maximum, should I use 2nd derivative test?
This would give 2R^2-3y (how do I show this is equal in to a negative value though?)
To find the maximum volume, would this be 2R^2-1/2y^3 * 2R/sqrt(3) ?
Is it 4R-3y?To apply the second derivative test, you just need to find the second derivative (which is not yet correct!), and then put your value for y into the formula for the second derivative. It will be obvious whether it is negative! (It will simplify to a numerical multiple of R.)
To find the max volume, put the value for y into the formula for V. What you show is not correct. (It will simplify to a multiple of R^3, and there will be no y in the answer, since that will have been replaced.)
Or -3y?Is it 4R-3y?
Yes. Remember, R is just a constant, whose derivative is zero. (If it were a variable, you'd have to use the chain rule! But it isn't.)Or -3y?
Am I right in saying this is equal to -6R/sqrt(3) ? [ . . . ]
It is a negative sign, therefore indicating it is a maximum (3*2R/sqrt(3)), which I believe would be equal to -6R/sqrt(3)?Back in your post # 3, with your positive stationary value, but with capital R, \(\displaystyle \ y = \ \dfrac{2R}{\sqrt{3}} \ cm.\)
The second derivative is \(\displaystyle \ -3y, \ \) which you gave in your post # 8, as the derivative with the R-variable is zero.
What is the sign of -3y with this y-value substituted into it? Does this sign indicate that the y-value is a maximum?
You must substitute the y-value in two places in the volume expression, given in part (b), and do some simplifying:
\(\displaystyle V \ = \ \bigg[\dfrac{2R^2}{1}\bigg(\dfrac{2R}{\sqrt{3}}\bigg) \ - \ \dfrac{1}{2}\bigg(\dfrac{2R}{\sqrt{3}}\bigg)^3\bigg] cm.^3\)
\(\displaystyle V \ = \ ? \ cm.^3 \)
